

Una Manera Sencilla para Probar un Teorema de Geometría Analítica
Enrique Vílchez Quesada
Universidad Nacional de Costa Rica
Escuela de Matemática
Resumen
La razón de esta propuesta, está fundamentada en brindar una exposición simple de una prueba de un teorema de geometría analítica, utilizado por nuestros estudiantes en la educación media y la educación media superior. Mi idea nació de la iniciativa de postular una demostración a un nivel básico, de tal forma que cualquier estudiante que conozca algunos principios generales de álgebra de polinomios, geometría analítica y trigonometría, pueda comprenderla sin mayor complicación.Este trabajo expone una demostración que corrobora que dos rectas son pa-ralelas cuando sus pendientes son iguales y son perpendiculares cuando el producto de ellas es igual a menos uno. El aspecto más trascendental, no consiste en la prueba que se realiza, ya que mediante los elegantes medios brindados por el álgebra lineal, la demostración cobra vida de una forma bastante natural, bajo un estilo que marchitaría mis esperanzas de poderla superar. Mi principal intención por tanto, consiste en exponer un ejemplo de un teorema usual dentro de la enseñanza secundaria, demostrado con conocimientos enmarcados dentro de esa línea. Este trabajo representa un esfuerzo por recordar a los colegas, la gran importancia de incorporar métodos de enseñanza que no abandonen la formalidad característica de la matemática como disciplina. Pedagógicamente ha existido y existe en la actualidad, la tendencia de incorporar metodologías de caracter inductivo, que conducen al estudiante a tener una expectativa equivocada con respecto al significado de un verdadero razonamiento lógico matemático.
Sean

 y
y

 dos rectas cuyas ecuaciones asociadas vienen dadas repectivamente por:
dos rectas cuyas ecuaciones asociadas vienen dadas repectivamente por:
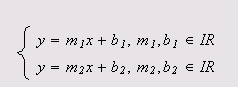
entonces:








En la siguiente prueba, los ángulos utilizados deben ser entendidos como ángulos euclideanos y no ángulos en posición estandar.

 Debemos tomar en consideración dos casos, a saber:
Debemos tomar en consideración dos casos, a saber:
Caso

 :
:

 Sean dos rectas
Sean dos rectas



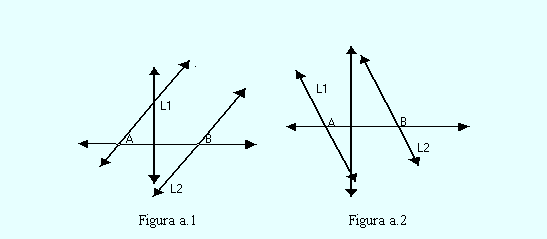
 dispuestas como se observa en la Figura a.1
entonces:
dispuestas como se observa en la Figura a.1
entonces:


 Por hipótesis:
Por hipótesis:

Caso

 :
:

 Sean dos rectas
Sean dos rectas



 dispuestas como se observa en la Figura a.2
entonces:
dispuestas como se observa en la Figura a.2
entonces:


 Por hipótesis:
Por hipótesis:


 Debemos tomar en consideración dos casos, a saber:
Debemos tomar en consideración dos casos, a saber:
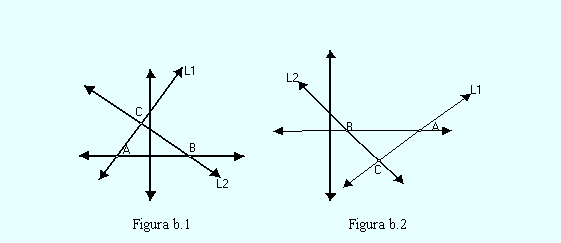
Caso

 :
:



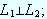


 Por hipótesis, sabemos que:
Por hipótesis, sabemos que:
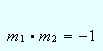
Por otra parte, es claro que:
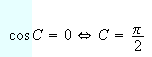
Dado que

 pues es un ángulo interno del
pues es un ángulo interno del

 .
Probemos que:
.
Probemos que:
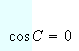

Caso 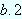

La prueba de este caso es idéntica a la realizada en b.1.
La matemática es una disciplina con una tendencia netamente teórica, como docente considero que en muchas instituciones educativas de enseñanza media, los colegas utilizan métodos de aprendizaje que pierden este principio, conduciendo a los educandos a aprender fórmulas sin ningún sentido científico. Este trabajo busca exponer un ejemplo de una prueba semiformal, que podría ser adaptada para la enseñaza en los salones de clase en secundaria.
Barrantes, H.

 .
Elementos de Álgebra Lineal. Editorial EUNED. Costa Rica.
.
Elementos de Álgebra Lineal. Editorial EUNED. Costa Rica.
Grossman, S.

 .Álgebra
Lineal. Editorial McGraw Hill. México.
.Álgebra
Lineal. Editorial McGraw Hill. México.
Meneses, R.

 .
Enseñanza y Aprendizaje de la Matemática Quinto
Año. Editorial Norma. Costa Rica.
.
Enseñanza y Aprendizaje de la Matemática Quinto
Año. Editorial Norma. Costa Rica.
Riddle, D.

 .Geometría Analítica. Editorial Thomson. México.
.Geometría Analítica. Editorial Thomson. México.
Swokowski, E.

 .
Álgebra y Trigonometría con Geometría
Analítica. Editorial Iberoamericana. México.
.
Álgebra y Trigonometría con Geometría
Analítica. Editorial Iberoamericana. México.
Revista Virtual, Matemática
Educación e Internet.
Derechos Reservados.