1 2 3 4 5 6

Elaboración de programas para GAE

Vamos ahora a analizar una conjuntos de programas para la GAE en álgebra elemental. El propósito de estudiarlos es que el lector intente emplear estas ideas en otros problemas de matemáticas de su interés. Mathematica nos permite presentar los resultados de estos programas de distintas formas. De hecho, podemos usar Mathematica como un editor de textos para la confección de un examen o prueba. Sin embargo, en este trabajo se intentará dar la salida de los programas para la GAE, de forma tal que su transición a código LATEX o TEX sea sencilla.

  1. Un problema clásico en trigonometría es el trabajar con ternas pitagóricas. Por su formación, un profesor de matemáticas conoce algunos ejemplos clásicos de ternas pitagóricas, no obstante, para confeccionar ejercicios interesantes es deseable que cuente con una fuente más amplia de estas cantidades. Hagamos un programa en Mathematica que nos permita hallar aleatoriamente ternas pitagóricas cuyos valores oscilen entre 2 y 40. El código del programa es el siguiente:
    ok = True;
While[ok == True,
  a = Random[Integer, {2, 40}];
  b = Random[Integer, {2, 40}];
  c = Random[Integer, {2, 40}];
   If[c^2 == a^2 + b^2,  ok = False]
  ]
Print["{(", a, ",", b,  ",", c ")}" ]
    La variable ok nos permite determinar si se ha hallado o no una terna pitagórica. Dicha variable se mantendrá con valor de verdad igual a True toda vez que no se haya conseguido el resultado esperado. Las asignaciones
      a = Random[Integer, {2, 40}];
  b = Random[Integer, {2, 40}];
  c = Random[Integer, {2, 40}];
    generan tres números enteros aleatorios cuyos valores se encuentra entre 2 y 40. Preguntamos luego si dichos números satisfacen la igualdad pitagórica 

    c^2 == a^2 + b^2 o bien c2 = a2 + b2. En el caso de que la terna sea pitagórica se hace la variable ok=False. La buena programación insta a garantizar que los ciclos que se programen, eventualmente terminen. Nosotros hemos obviado este detalle. Si el rango en que se buscan los números es "amplio" y la computadora es "rápida", el programa dará una respuesta casi instantánea. Además en el menú de Mathematica denominado kernel existe una opción llamada abort evaluation que puede suspender la ejecución del programa. Una solución un poco más elegante es definir un contador que registre cuántas iteraciones se han llevado a cabo y que dé por terminado el proceso si se excede un número de iteraciones preestablecidas. Con el fin de simplificar el código de los programas, en este ejemplo y en los siguientes, nos abstendremos de esta práctica.

    Al ejecutar el programa anterior, obtenemos en un caso {(20, 15, 25)}. Con el código presentado, no hay garantía de que esta tripleta vuelva a aparecer en una futura corrida del programa. Por supuesto es posible modificar el código para que se determine si esto ocurre o no. No obstante, esta mejora, en muchas ocasiones, no es necesaria y también la omitiremos.

  2. Consideremos ahora el problema de calcular el área de un triángulo rectángulo cuando conocemos (respectivamente) las proyecciones x y y de los catetos a y b sobre la hipotenusa c. Tratemos de confeccionar un ejercicio en el que todas las cantidades involucradas sean enteras, las longitudes de las proyecciones estén entre las 2 y 200 unidades y el área sea inferior a 1000 unidades cuadradas. El código es el siguiente:

    ok = True;
EsT[a_, b_, c_] := And[a + b > c, a + c > b, b + c > a]
While[ok == True,
  x = Random[Integer, {2, 200}];
  y = Random[Integer, {2, 200}];
  a = Sqrt[x(x + y)];
  b = Sqrt[y(x + y)];
  h = Sqrt[x y];
  area = (x + y) h /2;
   If[And[ area == Round[area], area < 1000, area != x y, x < y,
      EsT[a, x, h], EsT[b, h, y], EsT[a, b, y + x] ] , ok = False]
  ]
Print["{", x, "}{", y,  "}{", area, "}"]
    En este caso empezamos definiendo una función llamada EsT que se encarga de regresar True si los valores a, b y c satisfacen la desigualdad triangular y False en el caso contrario. Se supone además que EsT se aplicará solo a cantidades positivas. La variable ok se inicia en True y se mantiene así toda vez que no se cumplan las condiciones posteriormente estipuladas. En cada iteración del ciclo se generan dos candidatos para ser las proyecciones deseadas. De ser así se cumplirá entonces que a = 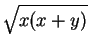$\displaystyle \sqrt{x(x + y)}$ y b = y(x + y). Además la altura sobre la hipotenusa estará dada por h = $\displaystyle \sqrt{xy}$.

    Veamos las condiciones. Para que el área se entera se debe cumplir que al aplicar la función Round, se obtenga el mismo valor. La condición area < 1000 es clara. La restricción area $\displaystyle \neq$ x se agrega pues después de varias corridas, esta situación (no deseada) ocurría con demasiada regularidad. Con el propósito de estar seguros que los valores generados realmente tienen sentido (además de ejemplificar el uso de las funciones), aplicamos entonces la función EsT a los 3 triángulos involucrados.

    Una salida típica de este programa es   {4}{9}{39}.

  3. Consideremos el problema de elaborar ejercicios en los que se deba resolver ecuaciones de la forma (ax + b)(cx + d )= f  y en la que los valores enteros involucrados tengan valor absoluto menor que 9. El código es el siguiente:
    c1 = Random[Integer, {-8, 8}];
c2 = Random[Integer, {-8, 8}];
c3 = Random[Integer, {-8, 8}];
c4 = Random[Integer, {-8, 8}];
ecua = (c1 x + c2)(c3 x + c4) == c2 c4
sol = Solve[ecua, x]
    Primero generamos los coeficientes, después construimos la ecuación y finalmente la resolvemos. Si tuviéramos algún interés en controlar el tipo de solución, podemos insertar este código en un ciclo y agregar ahí los requisitos deseados.

    En una corrida típica obtenemos (2 - 4x)(- 8 - 3x) = - 16 cuya solución está dada por x = - $\displaystyle {\textstyle\frac{13}{6}}$ y x = 0.

  4. Veamos ahora el problema de elaborar un programa que genere y resuelva ecuaciones de primer grado en x pero que contenga además otros parámetros o variables. El código es el siguiente:
    fl1 = x  y^(Random[Integer, {0, 2}])z^(Random[Integer, {0, 2}]);
fl2 = a^(Random[Integer, {0, 2}])  b^(Random[Integer, {0, 2}])
        c^(Random[Integer, {0, 2}]);
ld = Random[Integer, {1, 8}] fl1 + Random[Integer, {-8, 8}] fl2;
li = Random[Integer, {1, 8}] fl1 + Random[Integer, {-8, 8}] fl2;
ecua = li == ld
sol = Solve[ecua, x]
    La primera instrucción se encarga de generar un factor literal que contenga la variable x y que pueda contener las variables y y z hasta grado 2 inclusive. Al incluir el 0 en rango de la función Random, esto hace que eventualmente la variable y o z no aparezcan. El lado derecho de la ecuación ld se construye combinando los factores literales fl1 fl2. Análogamente se procede con el lado izquierdo de la ecuación, li. Finalmente se resuelve la ecuación desarrollada.

    En una corrida típica se genera - bc + xy = 8bc + 7xy con solución x = - $\displaystyle {\frac{3bc}{2y}}$.

  5. Suponga que deseamos construir ejercicios en los que el problema es, dados los lados de un triángulo cualquiera, hallar la suma de las alturas de dicho triángulo. Se requiere que los lados sean todos diferentes entre sí y que el área no exceda las 800 unidades cuadradas. El código es el siguiente:
    ok = True;
EsT[a_, b_, c_] := And[a + b > c, a + c > b, b + c > a]
While[ok == True,
  a = Random[Integer, {2, 200}];
  b = Random[Integer, {2, 200}];
  c = Random[Integer, {2, 200}];
  s = (a + b + c)/2;
  area = Sqrt[Abs[s(s - a)(s - b)(s - c)]];
  hab = 2 area/c;
  hac = 2 area/b;
  hbc = 2 area/a;
  sh = hab + hac + hbc;
   If[And[Denominator[sh] < 5, a != b, b != c, a != c, area < 800,
      EsT[a, b, c] ] , ok = False]
  ]
Print["{", a, "}{", b, "}{",  c, "}{", sh, "}"]
    La función Est es la misma que se empleó en el ejemplo 2. La variable ok es para mantenerse en el ciclo toda vez que no se satisfagan las condiciones deseadas.

    Iniciamos generando tres candidatos para las medidas del $\displaystyle \triangle$ABC en cuestión. El lado con media a se opone a $\displaystyle \angle$A y así sucesivamente con los otros elementos. La idea es aplicar la fórmula de Herón:

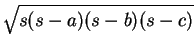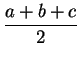    A = $\displaystyle \sqrt{s(s - a)(s - b)(s - c)}$, en donde s = $\displaystyle {\frac{a+b+c}{2}}$.

    Designamos con hab la altura sobre el lado $\displaystyle \overline{AB}$. Como la medida del lado AB es c entonces el área del triángulo se puede calcular como  

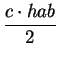    A = $\displaystyle {\frac{c\cdot hab}{2}}$, y por lo tanto, hab = $\displaystyle {\frac{2 \cdot A}{c}}$. Esto explica las instrucciones hab = 2area/c;, hac = 2area/b; y hbc = 2area/a;. Con el fin de que la expresión correspondiente a la suma de las alturas tenga un aspecto no muy complejo, solicitamos que el denominador de esta suma no sea mayor que 5. Pedimos además que a $\displaystyle \neq$ b, b $\displaystyle \neq$ c, a $\displaystyle \neq$ c y que el área sea inferior a las 800 unidades cuadradas.

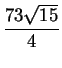
    Una corrida típica de este programa arroja $\displaystyle \left\{\vphantom{24 }\right.$24$\displaystyle \left.\vphantom{24 }\right\}$$\displaystyle \left\{\vphantom{32 }\right.$32$\displaystyle \left.\vphantom{32 }\right\}$$\displaystyle \left\{\vphantom{ 28}\right.$28$\displaystyle \left.\vphantom{ 28}\right\}$$\displaystyle \left\{\vphantom{ \frac{73\sqrt{15}}{4}}\right.$$\displaystyle {\frac{73\sqrt{15}}{4}}$$\displaystyle \left.\vphantom{ \frac{73\sqrt{15}}{4}}\right\}$

  6. Desarrollemos ahora un programa para generar un ejercicio de selección única en el que se debe colocar la solución correcta en la opción A y distractores en las otras opciones. En este caso vamos a generar código TEX. El código del programa es el siguiente: 
    x = Random[Integer, {-10, 20}]/Random[Integer, {3, 20}];
y = Random[Integer, {-10, 20}]/Random[Integer, {3, 20}];
Print["Ejercicio sumar:"]
Print["@frac{", Numerator[x], "}{", Denominator[x], "}+
@frac{", Numerator[y], "}{", Denominator[y], "}"]
z = x + y;
Print["Opcion A:"]
Print["@frac{", Numerator[z], "}{", Denominator[z], "}"]
z = Max[x, y] - Min[x, y];
Print["Opcion B:"]
Print["@frac{", Numerator[z], "}{", Denominator[z], "}"]
z = Max[x, y]*Min[x, y];
Print["Opcion C:"]
Print["@frac{", Numerator[z], "}{", Denominator[z], "}"]
z = x/y;
Print["Opcion D:"]
Print["@frac{", Numerator[z], "}{", Denominator[z], "}"]
    Iniciamos generando dos fracciones x y y. Tanto el numerador de x como y son valores entre -10 y 20. Los denominadores son valores entre 3 y 20. Mathematica se encarga de simplificar la fracción, en el caso de que sea necesario. Usamos @ en lugar del \ debido a que el caracter \f es una instrucción especial de Mathematica. Una vez generado el código, se debe realizar un proceso de encuentre/reemplace para convertir @frac en \frac.

    La opción correcta es z = x + y. Usando las funciones Numerator y Denominator para tomar el numerador y el denominador de las expresiones involucradas. En la segunda opción se toma la diferencia entre el máximo de x y y y mínimo de los mismos. En la opción siguiente se usa como distractor el producto entre el máximo y el mínimo de x y y. En la última opción se usa como distractor el cociente entre x y y. En este último caso, Mathematica se encarga de efectuar la simplificación correspondiente.

    Una salida típica de este programa es: 

    Ejercicio sumar:
@frac{ -1 }{ 16 }+@frac{ 19 }{ 10 }
Opcion A:
@frac{ 147 }{ 80 }
Opcion B:
@frac{ 157 }{ 80 }
Opcion C:
@frac{ -19 }{ 160 }
Opcion D:
@frac{ -5 }{ 152 }
    Este código lo podemos arreglar convenientemente para obtener el siguiente ítem. Observe.

    Al efectuar la suma - $\displaystyle {\textstyle\frac{1 }{16 }}$ + $\displaystyle {\textstyle\frac{19 }{10 }}$, obtenemos:

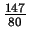
    1. $\displaystyle {\textstyle\frac{147 }{80 }}$
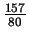
    2. $\displaystyle {\textstyle\frac{157 }{80 }}$
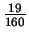
    3. - $\displaystyle {\textstyle\frac{19 }{160 }}$
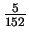
    4. - $\displaystyle {\textstyle\frac{5 }{152 }}$

  7. El siguiente programa está diseñando para generar ejercicios que evaluen el tema de producto de 2 monomios. Observe: 
    exp1 = Random[Integer, {-2, 2}] a + Random[Integer, {-8, 8}] b + Random[Integer, {-8, 8}] c
exp2 = Random[Integer, {-2, 2}] a + Random[Integer, {-8, 8}] b + Random[Integer, {-8, 8}] c
f1 = Random[Integer, {-5, 5}] x^(exp1)
f2 = Random[Integer, {-5, 7}] x^(exp2)
expre = f1 f2
    Comenzamos construyendo los exponentes de los monomios. Para ello usamos las variables exp1 y exp2. Seguidamente formamos los monomios f1 y f2. Seguidamente efectuamos el producto que, como sabemos, Mathematica se encarga de simplificar.

    Una corrida típica de este programa nos produce un ejercicio tal como

     3x2 a - 6 b - 5 c . 5 x-a + 4 b + 5 c = 15 xa - 2 b

  8. Consideremos ahora el problema de elaborar un ejercicio que desarrolle y simplifique una expresión polinomial de la forma P(Q - R), en la que P, Q y R son polinomios. Si deseamos además que la respuesta de este ejercicio no sea demasiado larga, vamos a requerir que la longitud de la expresión resultante no exceda los 4 términos. El código es el siguiente: 
    ok = True;
While[ok == True,
  p = Random[Integer, {2, 4}];
  q = Random[Integer, {2, 4}];
  r = Random[Integer, {2, 4}];
  P = Sum[(Random[Integer, {-4, 4}])x^k, {k, 0, p}] ;
  Q = Sum[(Random[Integer, {-4, 4}])x^k, {k, 0, q}];
  R = Sum[(Random[Integer, {-4, 4}])x^k, {k, 0, r}] ;
  W = Expand[P (Q - R)];
   If[Length[W] < 5, ok = False];
  ]
P
Q
R
W
    Como de costumbre, la variable ok nos mantiene en el ciclo mientras no se hallado el resultado solicitado. Comenzamos definiendo el grado de los polinomios con los que vamos a trabajar. Estos grados se hallan entre 2 y 4. Usando el comando Sum construimos los polinomios P, Q y R. En W almacenamos el resultado de desarrollar P(Q - R). Como no queremos que W exceda los 4 términos, nos mantenemos en el ciclo toda vez que su longitud sea mayor o igual que 4.

    Una corrida típica del programa genera un ejercicio como:

    P = 1 - x - 2 x2, Q = - 1 - x - x2, R = 3 - 3 x - x2, P(Q - R) = - 4 + 6 x + 6 x2 - 4 x3

  9. Desarrollemos ahora un programa que nos permita evaluar la aplicación de la ley de los cosenos. Vamos a construir un triángulo acutángulo en el que sus lados miden a, b y c unidades respectivamente. Además a < b < c. El ejercicio consiste en proporcionar solo a, b y el ángulo contenido por ambos lados que llamaremos g. El estudiante debe calcular la longitud del lado faltante, a saber c. Si desea elaborar un ejercicio de selección única, vamos a agregar 3 distractores sumando o restando un algún valor que se halle entre 1 y 10. El código es el siguiente: 
    ok = True;
While[ok == True,
  a = Random[Integer, {1, 200}];
  b = Random[Integer, {1, 200}];
  c = Random[Integer, {1, 200}];
   If[And[a < b + c, b < a + c, c < a + b, a < b, b < c,  c^2 < a^2 + b^2] ,
    ok = False]
  ]
Datos
a
b
g = ArcCos[c^2 - a^2 - b^2/(-2 a b)];
g 180.0/Pi
Respuesta
c
Distractores
d1 = c + (-1)^(Random[Integer, {0, 1}]) * Random[Integer, {1, 10}]
d2 = c + (-1)^(Random[Integer, {0, 1}]) * Random[Integer, {1, 10}]
d3 = c + (-1)^(Random[Integer, {0, 1}]) * Random[Integer, {1, 10}]
    Después de generar valores aleatorios entre 1 y 200 para las variables a, b y c, verificamos la desigualdad triangular, comprobamos que a < b < c y que el triángulo generado sea acutángulo. Usando la ley de cosenos obtenemos el ángulo que se opone al lado c. La información que suministramos al estudiante es entonces a, b y g. La respuesta es c. Seguidamente calculamos 3 distractores d1, d2 y d3 usando la función Random.

  10. Consideremos ahora el problema de generar desigualdades lineales estrictas con algunos coeficientes fraccionarios. Esencialmente lo que hacemos es generar una desigualdad, resolver la ecuación correspondiente, evaluar en un valor a la izquierda de la solución y con base en esto, establecer la solución. La respuesta se da usando TEX. El código es el siguiente: 
    c1 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
c2 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
c3 = Random[Integer, {-8, 8}];
c4 = Random[Integer, {-8, 8}];
c5 = Random[Integer, {-8, 8}];
c6 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
c7 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
c8 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
c9 = Random[Integer, {-8, 8}]/Random[Integer, {1, 1}];
 If[Random[] < 0.5,
     d = c4(c1 x + c2) + c5(c6 x + c7) < c3(c8 x + c9)  ,
    d = c4(c1 x + c2) + c5(c6 x + c7) > c3(c8 x + c9)]
RD = Module[{li, ld, s, t},
                      li = d[[1]];
                      ld = d[[2]];
                      s = Solve[li == ld][[1]][[1]][[2]];
                      Print[s];
                      t = s - 1;
                      If[d /. x -> t,
                          TeXForm["{", d, "}{", x < s, "}"],
                          TeXForm["{", d, "}{", x > s, "}"]
                      ]]
    En este último ejemplo no vamos a explicar con detalle el código, esto con el propósito de dejarlo como ejercicio para el lector.

    Una corrida típica de este programa proporcionó el siguiente resultado: 

    {,8\,\left( -6 - 3\,x \right)  > 7\,\left( -7 - 2\,x \right) ,}{,x < \frac{1}{10},}
    Después de arreglarlo convenientemente obtenemos:

    8( -6 - 3 x) > 7(-7 - 2 x) con solución x < $\displaystyle {\textstyle\frac{1}{10}}$,

1 2 3 4 5 6

Revista Matemática, Educación e Internet

Derechos Reservados