|
1
2
Curvas de Bezier
Usando las definiciones anteriores podemos definir las curvas de Bezier directamente en Mathematica:
In[68]:=
![Bezier[pts_] := Bernstein2[Length[pts] - 1] . pts ;](imagenes/index_90.gif)
en donde pts es una familia finita de pares ordenados de 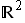 . Además, en . Además, en ![Bernstein2[Length[pts] - 1] . pts](imagenes/index_92.gif) , el punto
(.) denota el producto matricial, aunque puede significar muchas cosas dependiendo de los operandos que usemos (multiplicación de matrices, producto escalar, etc.). En este caso es una multiplicación de matrices cuyo resultado es una matriz 1×2. Visualicemos esto mediante el siguiente ejemplo en el que se construye un as de espadas, aunque no del todo terminado. , el punto
(.) denota el producto matricial, aunque puede significar muchas cosas dependiendo de los operandos que usemos (multiplicación de matrices, producto escalar, etc.). En este caso es una multiplicación de matrices cuyo resultado es una matriz 1×2. Visualicemos esto mediante el siguiente ejemplo en el que se construye un as de espadas, aunque no del todo terminado.
In[213]:=
![p1 = {{-0.144, -0.830}, {-0.069, -0.588}, {-0.037, -0.253}} ; AsespadasPlot1 = Bezier[p1] ; p2 ... e[7], RGBColor[1, 0, 0], Point /@ Join[p1, p2]}], Axes -> True, AspectRatio -> Automatic] ;](imagenes/index_93.gif)
![[Graphics:HTMLFiles/index_94.gif]](imagenes/index_94.gif)
Figura 3: As de espadas.
![AsespadasPoints = Module[{LeftSide}, LeftSide = Join[AsespadasPlot1[[1, -1, 1, 1]], Asespadas ... * # &, LeftSide]]]] ; Sow[Graphics[Polygon[AsespadasPoints]], AspectRatio -> Automatic] ;](imagenes/index_95.gif)
Si tenemos una función ![f : [0, 1] --> ÷µ](imagenes/index_96.gif) y una familia finita de puntos y una familia finita de puntos 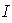 dada por dada por
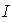 = { = {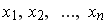 } donde } donde 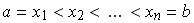
obtenemos una familia de puntos de la forma:
{(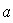 , ,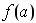 ,( ,(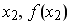 ), ..., ( ), ..., (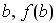 )} )}
Observemos con cuidado que hace Bezier, ejemplificado para el caso de una partición uniforme, por comodidad.
![n = 5 ; puntos = Table[{a + k * (b - a)/n, f[a + k * (b - a)/n]}, {k, 0, n}] ; Bezier[puntos] // Expand ; %[[1]] %%[[2]] // Simplify](imagenes/index_105.gif)
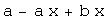
![-(-1 + x)^5 f[a] + x (-10 (-1 + x)^3 x f[(3 a)/5 + (2 b)/5] + 10 (-1 + x)^2 x^2 f[(2 a)/5 + (3 ... 0 x^3 f[1/5 (4 a + b)] + 5 x^4 f[1/5 (4 a + b)] + 5 x^3 f[1/5 (a + 4 b)] - 5 x^4 f[1/5 (a + 4 b)])](imagenes/index_107.gif)
La primera componente nos define una parametrización lineal de ![[0, 1] --> [a, b]](imagenes/index_108.gif) , mientras que la segunda componente nos da , mientras que la segunda componente nos da ![Bernstein[n, f[a + b(x - a)], x ]](imagenes/index_109.gif) , para , para ![x ∈ [0, 1]](imagenes/index_110.gif) . .
El teorema fundamental nos dice que si ![f : [a, b] --> ÷µ](imagenes/index_123.gif) es una función de clase es una función de clase 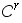 y y 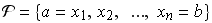 es una partición de es una partición de ![[a, b]](imagenes/index_126.gif) , entonces existe un trazador (q,r) que interpola a , entonces existe un trazador (q,r) que interpola a 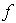 hasta el orden hasta el orden 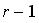 , en los puntos , en los puntos 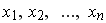 (en los puntos (en los puntos 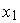 y y 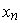 a veces se dan otras condiciones). a veces se dan otras condiciones).
Mathematica tiene varios paquetes útiles como Numerical Math 'SplineFit' el cual es un programa no tan general como Interpolating polynomial; es una implementación en Mathematica del algoritmo presentado por Burden ([3]), para el caso de trazadores cúbicos. No esta diseñado para el caso n-dimensional,  . .
Construyamos un ejemplo sencillo. Pero observemos los tipos de trazadores: Type-Cubic, CompositeBezier y Bezier.
In[186]:=
![Clear[n, k] ; puntos1 = Table[{-2 + k/n, 1/(1 + 12 * (-2 + k/n))}, {k, 0, 6}] /. n -> 6](imagenes/index_133.gif)
Out[187]=
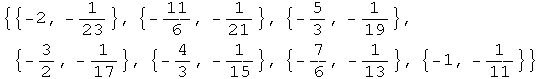
En dichos puntos estamos haciendo un muestreo de la función 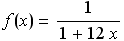 en en ![[-2, -1]](imagenes/index_136.gif) . .
In[196]:=
![<< NumericalMath`SplineFit` gg = SplineFit[puntos1, Cubic] gg[x] Print["Primer valo ... abla de puntos"] ; gg[0] Print["Sexto valor de la tabla de puntos"] gg[6] gg[5.25]](imagenes/index_137.gif)
Out[197]=
![SplineFunction[ Cubic , {0.`, 6.`} , <>]](imagenes/index_138.gif)
Out[198]=
![(SplineFunction[ Cubic , {0.`, 6.`} , <>])[x]](imagenes/index_139.gif)
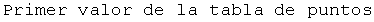
Out[200]=
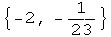
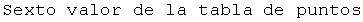
Out[202]=
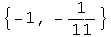
Out[203]=
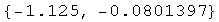
![gg[x]](imagenes/index_145.gif) define una función cuyo dominio es un intervalo cerrado que inicia en el primer define una función cuyo dominio es un intervalo cerrado que inicia en el primer 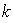 de la tabla, en este caso 0, y finaliza en el último valor de de la tabla, en este caso 0, y finaliza en el último valor de 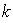 , en este caso 6. , en este caso 6.
![gg : [0, 6] --> ÷µ^2](imagenes/index_148.gif) cuya segunda componente es la aproximación por trazadores cúbicos de cuya segunda componente es la aproximación por trazadores cúbicos de 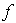 . Para que nos sea útil tenemos que convertirla en una función definida sobre el intervalo . Para que nos sea útil tenemos que convertirla en una función definida sobre el intervalo ![[-2, -1]](imagenes/index_150.gif) lo cual hacemos parametrizando linealmente; en este caso con lo cual hacemos parametrizando linealmente; en este caso con 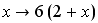 . .
Usando Mathematica
In[204]:=
![ggg[x_] := gg[6 * (2 + x)][[2]] ; Plot[{ggg[x], 1/(1 + 12 x)}, {x, -2, -1}, PlotStyle -> {R ... ; {PointSize[0.03], Table[Point[{-2 + k/n, 1/(1 + 12 * (-2 + k/n))}], {k, 0, 6}] /. n -> 6}] ;](imagenes/index_152.gif)
![[Graphics:HTMLFiles/index_153.gif]](imagenes/index_153.gif)
Figura 4: Gráficas de las funciones
ggg[x] y f[x].
Las gráficas de ambas funciones ![ggg[x]](imagenes/index_154.gif) y y 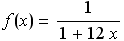 coinciden. coinciden.
In[206]:=
![hh[t_] := Bezier[puntos1] /. x -> t ; hh[-2] hh[0] hh[1] Clear[hhh] ; hhh[x_] := hh[2 + x][ ... hh[x]}, {x, -2, -1}, PlotStyle -> {RGBColor[0, 0, 1], RGBColor[0, 0, 1], RGBColor[1, 0, 0]}] ;](imagenes/index_156.gif)
Out[207]=
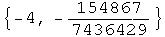
Out[208]=
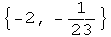
Out[209]=
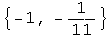
![[Graphics:HTMLFiles/index_160.gif]](imagenes/index_160.gif)
Figura 5: Gráficas de las
funciones ggg[x], f[x] y hhh[x].
Las gráficas de color azul corresponde a las funciones ![ggg[x]](imagenes/index_161.gif) y y 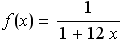 , las cuales coinciden. La gráfica de color rojo corresponde a la función , las cuales coinciden. La gráfica de color rojo corresponde a la función ![hhh[x]](imagenes/index_163.gif) , generada con Bezier. , generada con Bezier.
Bibliografía
[1] Araya Aguilar, Gerardo. Solución a algunos problemas de Korovkin. (1982), UCR, Costa Rica.
[2] Borwein, P.; T. Erdelyi. Polinomials and polinomial inequalities. (1996), SIAM Review, vol 38, # 4. pp. 705-706.
[3] Burden, Richard; Douglas Faires. Análisis numérico. Editorial Iberoamérica, México, 1985.
[4] Chui, C. K.; L. Schumaker; J. D. Wardor. Approximation theory V. (1988). Mathematics of computatino, vol 50, # 181. pp. 356.
[5] Gamelin, T. W.; R. E. Greene. Introduction to topology. (1986), American Mathematical Monthly, vol. 93, # 7. pp. 580-582.
[6] Sendov, Blagovet; Vasil A. Popov; G. M. Phillips. The averaged moduli of smoothness:with applications in numerical methods and approximation. (1991) SIAM Review, vol. 33, #3. pp. 499-501.
|
![p1 = {{-0.144, -0.830}, {-0.069, -0.588}, {-0.037, -0.253}} ; AsespadasPlot1 = Bezier[p1] ; p2 ... e[7], RGBColor[1, 0, 0], Point /@ Join[p1, p2]}], Axes -> True, AspectRatio -> Automatic] ;](imagenes/index_93.gif)
![[Graphics:HTMLFiles/index_94.gif]](imagenes/index_94.gif)
![AsespadasPoints = Module[{LeftSide}, LeftSide = Join[AsespadasPlot1[[1, -1, 1, 1]], Asespadas ... * # &, LeftSide]]]] ; Sow[Graphics[Polygon[AsespadasPoints]], AspectRatio -> Automatic] ;](imagenes/index_95.gif)
![n = 5 ; puntos = Table[{a + k * (b - a)/n, f[a + k * (b - a)/n]}, {k, 0, n}] ; Bezier[puntos] // Expand ; %[[1]] %%[[2]] // Simplify](imagenes/index_105.gif)
![-(-1 + x)^5 f[a] + x (-10 (-1 + x)^3 x f[(3 a)/5 + (2 b)/5] + 10 (-1 + x)^2 x^2 f[(2 a)/5 + (3 ... 0 x^3 f[1/5 (4 a + b)] + 5 x^4 f[1/5 (4 a + b)] + 5 x^3 f[1/5 (a + 4 b)] - 5 x^4 f[1/5 (a + 4 b)])](imagenes/index_107.gif)
![Clear[n, k] ; puntos1 = Table[{-2 + k/n, 1/(1 + 12 * (-2 + k/n))}, {k, 0, 6}] /. n -> 6](imagenes/index_133.gif)
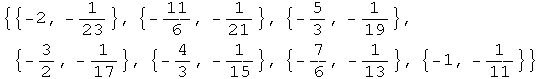
![<< NumericalMath`SplineFit` gg = SplineFit[puntos1, Cubic] gg[x] Print["Primer valo ... abla de puntos"] ; gg[0] Print["Sexto valor de la tabla de puntos"] gg[6] gg[5.25]](imagenes/index_137.gif)
![ggg[x_] := gg[6 * (2 + x)][[2]] ; Plot[{ggg[x], 1/(1 + 12 x)}, {x, -2, -1}, PlotStyle -> {R ... ; {PointSize[0.03], Table[Point[{-2 + k/n, 1/(1 + 12 * (-2 + k/n))}], {k, 0, 6}] /. n -> 6}] ;](imagenes/index_152.gif)
![[Graphics:HTMLFiles/index_153.gif]](imagenes/index_153.gif)
![hh[t_] := Bezier[puntos1] /. x -> t ; hh[-2] hh[0] hh[1] Clear[hhh] ; hhh[x_] := hh[2 + x][ ... hh[x]}, {x, -2, -1}, PlotStyle -> {RGBColor[0, 0, 1], RGBColor[0, 0, 1], RGBColor[1, 0, 0]}] ;](imagenes/index_156.gif)
![[Graphics:HTMLFiles/index_160.gif]](imagenes/index_160.gif)