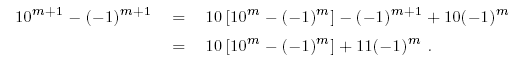| 1. |
algoritmo:
m. conjunto ordenado y finito de operaciones que permite hallar la
solución de un problema [2] |
| 2. |
La demostración rigurosa de esto es por inducción matemática.
Deseamos demostrar que, para cualquier entero 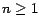 , , 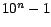 es divisible por 9 (lo cual
significa que cada término en la suma de es divisible por 9 (lo cual
significa que cada término en la suma de 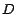 es divisible por 9).
Evidentemente esto es cierto en el caso es divisible por 9).
Evidentemente esto es cierto en el caso 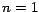 , porque , porque 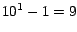 .
Asumamos ahora que es cierto si .
Asumamos ahora que es cierto si 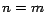 , para algún valor entero
arbitrario de , para algún valor entero
arbitrario de 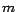 . En ese caso tenemos que . En ese caso tenemos que
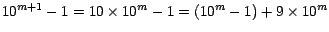 . Vemos inmediatamente que . Vemos inmediatamente que 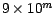 es divisible por 9. Por lo tanto si
es divisible por 9. Por lo tanto si 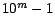 es divisible por 9, entonces es divisible por 9, entonces
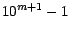 también debe serlo. Esto completa la demostración. también debe serlo. Esto completa la demostración. |
| 3. |
Claramente no importa si, en lugar de sumar los
dígitos en posición impar y restar los dígitos en posición
par, sumamos los de posición par y restamos los de posición impar,
porque si el resultado de la primera operación arroja el número 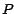 ,
el resultado de la segunda arroja ,
el resultado de la segunda arroja 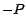 . Y . Y 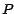 es divisible por un
número es divisible por un
número 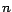 si y solo si si y solo si 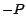 también los es. Lo importante al aplicar
la regla es alternar entre suma y resta de un dígito al siguiente. también los es. Lo importante al aplicar
la regla es alternar entre suma y resta de un dígito al siguiente.
|
| 4. |
Nuevamente, la prueba es por inducción
matemática. Deseamos demostrar que 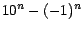 es divisible por 11,
para cualquier entero es divisible por 11,
para cualquier entero 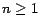 . Esto es cierto en el caso . Esto es cierto en el caso 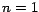 , ya que , ya que
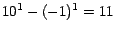 . Asumamos ahora que es cierto para . Asumamos ahora que es cierto para 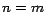 . .
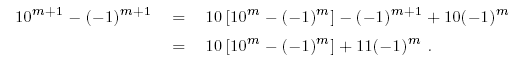
En el primer paso simultáneamente sumamos y restamos la
cantidad 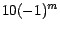 . Como . Como 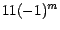 es divisible por once y asumimos que
la cantidad entre paréntesis cuadrados, es divisible por once y asumimos que
la cantidad entre paréntesis cuadrados,
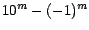 , es divisible
por 11, entonces , es divisible
por 11, entonces
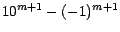 también debe serlo. Esto
completa la demostración por inducción. también debe serlo. Esto
completa la demostración por inducción.
|
| 5. |
El lector especialmente perspicaz e informado
notará que esto implica que si escribimos 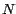 en la base en la base 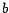 , es fácil
formular reglas de divisibilidad para , es fácil
formular reglas de divisibilidad para 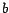 , , 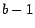 , , 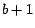 y los divisores
respectivos de esos números. Los lectores avanzados de este
artículo quizás desearán corroborar eso en el caso general,
usando como punto de partida las demostraciones que hemos ofrecido en el
caso de y los divisores
respectivos de esos números. Los lectores avanzados de este
artículo quizás desearán corroborar eso en el caso general,
usando como punto de partida las demostraciones que hemos ofrecido en el
caso de 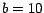 , que corresponde a la notación decimal ordinaria. , que corresponde a la notación decimal ordinaria.
|
| 6. |
Para aquellos que lo hayan olvidado, un número primo es
aquel entero que solo es divisible por 1 y por sí mismo.
|
| 7. |
El lector perspicaz se habrá percatado que hemos
introducido en la lógica de las reglas de divisibilidad la pequeña
variación de de escribir
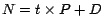 . Este método para saber si . Este método para saber si
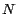 es divisible por es divisible por 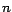 funciona si 1 es el máximo común divisor de funciona si 1 es el máximo común divisor de
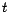 y y 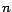 . Como en este caso específico . Como en este caso específico 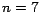 es primo, cualquier
valor de es primo, cualquier
valor de
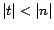 que nos diera un que nos diera un 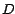 divisible
por divisible
por 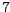 hubiera sido aceptable. El valor indicado para hubiera sido aceptable. El valor indicado para 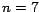 fue, como
hemos visto, fue, como
hemos visto, 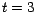 . .
|
| 8. |
El lector interesado puede demostrar, como ejercicio,
que este número 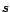 siempre existe, para cualquier siempre existe, para cualquier 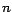 que cumpla las
condiciones que acabamos de especificar. que cumpla las
condiciones que acabamos de especificar. |
| |
|