Usos didácticos de la hoja electrónica Excel 

José Luis Espinoza B.

Escuela de Matemática
Instituto Tecnológico de Costa Rica. 
e-mail: jespinoza@itcr.ac.cr.

Resumen

En este artículo se presenta parte de la experiencia desarrollada en la Escuela de Matemática del Instituto Tecnológico de Costa Rica sobre la Enseñanza de Métodos Numéricos, aprovechando la disponibilidad casi generalizada de la hoja electrónica Excel. La programación de algoritmos se ha hecho con la incorporación de macros; además se presenta al lector la secuencia de instrucciones necesarias para la ejecución de los distintos métodos. Aunque en principio estos materiales corresponden a un curso de nivel universitario, puede utilizarse como idea inicial para adecuar algunos de los conceptos tratados a la enseñanza de la matemática a nivel de secundaria. Tal es el caso de la graficación de funciones, aprovechando la hoja electrónica para ilustrar conceptos de dominio, rango, amplitud y período de funciones trigonométricas, etc. 

Palabras clave: Funciones, aplicaciones didádicas de Excel, enseñanza de la matemática, software didáctico.

1. Introducción

El objetivo principal de este trabajo es difundir parte de la experiencia desarrollada por la Escuela de Matemática del Instituto Tecnológico de Costa Rica en uno de los enfoques que tenemos para la enseñanza de los métodos numéricos. Para la enseñanza de los distintos métodos y prácticas de laboratorio se ha utilizado MATLAB, así como Java para ponerlos en applets que funcionan en línea. Pero se ha tenido también la necesidad y oportunidad de programar los algoritmos mediante macros, desde una hoja electrónica Excel . 
Debido a que en Costa Rica y sin duda en muchos otros países, el Excel se encuentra instalado de forma casi generalizada en las computadoras personales y en los laboratorios de computadoras de la mayoría de instituciones educativas, se puede hacer uso de este tipo de soluciones a nivel de programación de algoritmos, sin necesidad de adquirir e instalar software adicional. Las ideas aquí planteadas pueden ser implementadas en su equivalente para otras plataformas, como Linux, pero he adoptado el enfoque basado en Excel solamente por la familiaridad que tengo con este software y no por ningún tipo de preferencia. 
Puede considerarse esta contribución como una primera versión, con muy poca programación de macros que harían más atractiva la aplicación, pero que requeriría de mayores destrezas de programación por parte del usuario, de tal forma que está dirigida a principiantes en el manejo de Excel como herramienta didáctica. 

2. Graficación de funciones

Vamos a ilustrar una de las formas en que se puede graficar en una hoja electrónica Excel con la función f(x) = 5cos(4x)+3, con x variando en el intervalo [-5,10]. La gráfica de esta función se presenta en la figura 1. Podemos hacerlo de tal forma que se permita cambiar los límites inferior y superior de este intervalo y que la gráfica se actualice inmediatamente. 
Para empezar, es conveniente ubicar los valores a y b del intervalo en dos celdas específicas; por ejemplo, digitando el valor –5 en la celda B3 y el valor 10 en la celda B4. Al hacerlo de esta forma, toda operación que dependa de los valores a y b, incluyendo la gráfica de f(x) se actualizará cuando cambiemos estos valores. 
También es conveniente definir una longitud de paso h y un número n de puntos a evaluar para formar los puntos (xi, f(xi)), con xi = a+ih, para i=0, 1, ..., n, h = (b-a)/n. En este caso, se puede dejar n fijo en 100 y calcular h, editándolo en la celda B6, como +(B4-B3)/100.
Ahora en la celda C5 iniciamos nuestro rango de valores de la variable x, editando el valor +B3. En la celda C6 editamos el valor +C6+B$6. El símbolo $ se utiliza para dejar fijo el número de fila. Esta celda se copia hacia abajo 100 veces o cualquier otra cantidad que se quiera, pero al hacerlo 100 veces estamos seguros de que vamos a graficar en el intervalo [a,b]. 
Una forma de introducir la función f(x) sería digitando la fórmula directamente en la celda D6: +5*COS(C6)+3. Luego se copia hacia abajo hasta completar la tabla de puntos (xi,f(xi)). La ventaja de introducir el criterio de f(x) de esta forma es que es más directa y asequible para el usuario habitual de Excel. La desventaja es que se introduce de una forma no tan cercana a la escritura matemática y puede resultar incómodo al tener que hacerlo en una celda, que aunque se extienda como renglón, ciertamente es un espacio muy reducido. 
Otra forma de introducir f(x) es mediante una caja de diálogo. A grandes rasgos, a la fórmula introducida se le aplica un corrector de sintaxis, seguido de un evaluador de funciones. Pero el enfoque que doy a continuación es mediante el uso de macros. En el contexto en que se programan los macros la edición de la función no se hace directamente en las celdas, sino en el editor de Visual Basic. Para definirla, se hace lo siguiente: 

1. 
   • En la opción Herramientas del menú, seleccionar Macros. 
   • Luego se elige Editor de Visual Basic.
   • En el menú Insertar, seleccionar Módulo y se escribe el siguiente código: 
          Function f(x)
                f = 5*Cos(x)+3
         End Function

Ahora se digita en la celda D6: +f(C6) en lugar de la forma en que se hizo antes, se copia hacia abajo, hasta completar el rango de puntos, produciendo exactamente el mismo efecto. 
Finalmente, marcamos el rango de puntos con sus dos coordenadas y hacemos uso del asistente para gráficos hasta obtener una gráfica como en la figura 1.

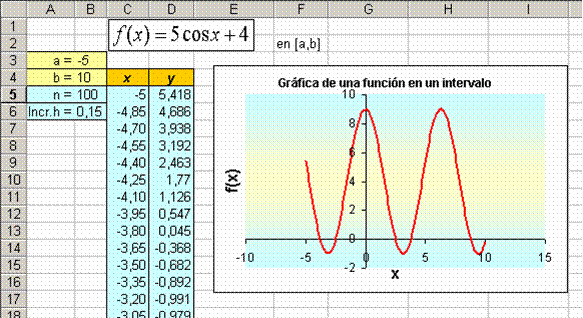
Fig. 1. Gráfica obtenida de f(x) = 5Cos(4x)+3.

Como es bien sabido, el uso adecuado de los colores es muy importante para llamar la atención de los estudiantes y para crear ambientes de enseñanza y aprendizaje más lúdicos. En este caso, sin pretender que se ha hecho la mejor escogencia de colores, se ha seguido la forma habitual en Excel para celdas o rangos de celdas, así como para el formato para gráficas. 
La gráfica de esta función en particular, puede servir para tratar temas como periodicidad, amplitud, dominio, ámbito, traslaciones verticales y horizontales, crecimiento, decrecimiento, máximos, mínimos, ceros de f(x), haciendo las variaciones que se requieran. La visualización gráfica que tenemos de la función también nos permite localizar intervalos en los que se halla una solución de la ecuación f(x) = 0. Por ejemplo, puede notarse que en el intervalo [3,5] existe un cero p de f(x), por lo que se puede redefinir el intervalo [a,b] como [3,5] para focalizar la gráfica (Ver figura 2) y luego aplicar algún método numérico para calcular en forma aproximada el valor de p.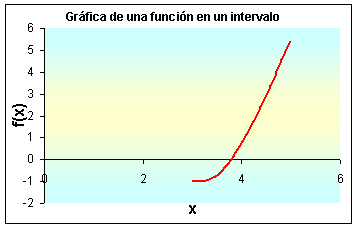 

Fig. 2. Focalización de la gráfica de f(x) = 5Cos(4x)+3 en el intervalo [3,5].

3. Solución de ecuaciones en una variable: El método de la bisección

Si una función f(x) es continua en un intervalo [a,b], en caso de que f(a) y f(b) tengan signos opuestos, es bien conocido que el Teorema de los Valores Intermedios asegura la existencia de una raíz p de f(x) en el intervalo [a,b]. Por ser el algoritmo de bisección uno de los métodos más sencillos de cálculo aproximado de raíces de funciones, se ha escogido éste para ilustrar la forma en que se pueden resolver una ecuación, de manera aproximada, en Excel. Para iniciar el proceso, se calcula el punto medio 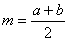. Luego se verifica, tal y como se hizo inicialmente para el intervalo [a,b], si el cambio de signo de f(x) ocurre en el intervalo [a,m] o en [m,b]. Si este cambio ocurre en el primer intervalo, se toma ahora el intervalo [a,b] como [a,m]; en caso contrario, se toma como [m,b]. Este proceso se repite sucesivamente, tomando como aproximación de la raíz el punto medio que se va obteniendo, hasta que el error de aproximación, que puede estimarse en la iteración enésima como , sea menor que una tolerancia específicada. 

4. Implementación del método de bisección en Excel

Vamos a ilustrar la forma en que se puede implementar en Excel el algoritmo de bisección con la función en el intervalo [-1,3]. Esta función, como puede notarse, es continua en dicho intervalo. 
Justamente en este caso se justifica editar g(x) en un macro, debido a la extensión de esta fórmula, pues si lo hiciéramos directamente en la celda C6, habría que digitar: 3 * LN (2+C5) + 2 * C5 ^ 3 - C5^2 - 2 * C5 - 20. 
En un macro, se escribe: 

                 Function g(x)

                    g = 3 * Log(2+x) + 2 * x^3 - x^2 - 2 * x - 20

               End Function

Para tener una idea de la gráfica de g(x) se procede a definir los extremos del intervalo, a=-1, b=3 y a evaluarla en las celdas correspondientes, tal y como se explicó para la función f(x).

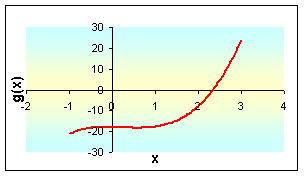
Fig. 3. Función .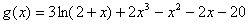

Al principio nuestra hoja electrónica luce más o menos así: 

Fig 4. Hoja electrónica para implementar el método de bisección.

Las celdas B5 y D5 contienen los valores extremos del intervalo [a,b] con que inicia el algoritmo. La celda B2 contiene el punto medio , por lo que se digita en esta celda +(B5+D5)/2. 
En la celda H5 se ha digitado la fórmula +(D5-C5)/2, que sirve como cota del error con que m aproxima al cero de g(x). 
En las celdas E5, F52 y G5 se ha digitado, respectivamente, +g(B5), +g(C5) y +g(D5), que corresponden a g(a), g(m) y g(b). 
Para decidir el nuevo intervalo en que queda encerrado el cero de g(x), cuyos extremos se van a escribir en las celdas B6 y D6:
En la celda B6,se escribe: +SI(g(B5)*g(C5)<0,B5,C5).
En la celda D6,se escribe: +SI(g(C5)*g(D5)<0,D5,C5).
Luego se copian los cálculos de la fila 5 que faltan en la fila 6. 
Finalmente, se copia todo el contenido de la fila 6 hacia abajo, tantas veces como sea necesario, hasta lograr la precisión deseada, para obtener la siguiente tabla de aproximaciones: 

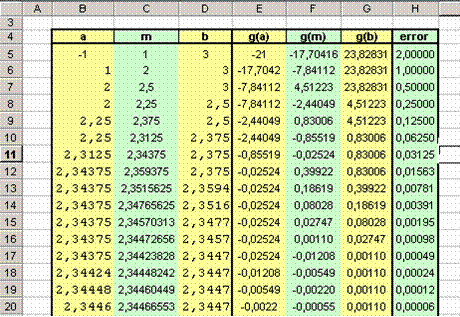
Figura 5: Resultado del método de bisección para resolver la ecuación
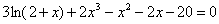en el intervalo [-1,3].

En la figura 5 se presentan los cálculos para la aproximación, finalizando con un error menor que 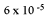. Una aproximación de un cero de g(x) sería el valor x=2.34466553, el cual se encuentra en la celda C20. 

Finalmente, cabe destacar que estas dos aplicaciones didácticas del Excel se han tomado a manera de ejemplo de la forma en que se puede utilizar la hoja electrónica en la enseñanza de muchos otros conceptos, no solamente a nivel universitario, sino también a nivel de enseñanza secundaria. 

5. Conclusiones. 

Podemos utilizar más ampliamente la hoja electrónica Excel o su equivalente en otros sistemas operativos para la enseñanza de conceptos matemáticos sin tener que recurrir a software adicional que incrementaría, tanto para el profesor como para el estudiante, el costo por licenciamiento y el tiempo dedicado a aprenderlo. Esta utilización puede ser desde muy sencilla, recurriendo a pocos recursos de programación, hasta mucho más sofisticada, en cuanto al ingreso de parámetros y formatos de salida y que requiere de más recursos de programación. 
El enfoque de esta contribución ha sido el de pocos recursos de programación, pero tratando de abrir el camino a una mayor profundización y diversificación por parte del usuario. 

Bibliografía: 

1. Burden, R.; Faires, D. Análisis Numérico. Ed. Thomson, 6a. ed., 1998.
2. De Levie, Robert. Advanced Excel for Sientific Data Analysis. Oxford University 
Press, 2004.
3. Liengme, B.; A Guide to Microsoft Excel 2002 for Scientists and Engineers. 
Butterworth Heinemann, 3rd, ed. 2002. 
4. Mathews, J; Fink, K. Métodos Numéricos con MATLAB. Prentice Hall, 3a. ed., 2000.
5. Press, W.; Teukolsky, S.; Vterling, W.; Flannery, B. Numerical Recipes in C. 
Cambridge University Press, 2nd ed., 1992.