Revista   1 2 3 4   

Matrices de rotación

Si A   es ortogonal (i.e. A^tA = I) y si $\lambda$ = 1   es un valor propio de A y u es un vector propio asociado a $\lambda$ = 1, entonces < Av,u > = < Av, Au > = < v,u >. Esto hace que Av y v tengan la misma norma y el mismo ángulo respecto a u. Av es una rotación de v alrededor de u.

En general, si A es ortogonal, Av es una rotación de v (algunas de estas rotaciones son `impropias', es decir, corresponden a reflecciones, inversiones o ``rotoreflecciones"). Ahora, dada A ortogonal, cuál es el ángulo de giro y cuál es el eje de giro?

TEOREMA (Matrices ortogonales)

Sea A_3×3 = (a_ij) real ortogonal

Sean $\omega$ y $\bar{\omega}$ complejos conjugados. Si $\lambda_{1}^{}$ = 1,  $\lambda_{2}^{}$ = $\omega$ y $\lambda_{3}^{}$ = $\bar{\omega}$ son los valores propios de la matriz A, entonces Av es una rotación de v, de ángulo $\phi$, alrededor de la recta generada por cualquier vector propio  u  asociado al valor propio $\lambda$ = 1. El ángulo de rotación $\phi$ satisface la ecuación cos($\phi$) = ${\frac{1}{2}}$(TrA - 1). Además podemos tomar

u = $$\left(\vphantom{\frac{a_{32}-a_{23}}{2 \mbox{sen} \phi},\, \frac... ...-a_{31}}{2 \mbox{sen} \phi},\, \frac{a_{21}-a_{12}}{2 \mbox{sen} \phi}}\right.$$$${\frac{a_{32}-a_{23}}{2 \mbox{sen} \phi}}$$, $${\frac{a_{13}-a_{31}}{2 \mbox{sen} \phi}}$$, $${\frac{a_{21}-a_{12}}{2 \mbox{sen} \phi}}$$$$\left.\vphantom{\frac{a_{32}-a_{23}}{2 \mbox{sen} \phi},\, \frac... ...-a_{31}}{2 \mbox{sen} \phi},\, \frac{a_{21}-a_{12}}{2 \mbox{sen} \phi}}\right)$$

 

$\bullet$

En la fórmula del teorema si $\phi$ = 0,   u   es indeterminado. Esto se considera razonable puesto que el eje de rotación pierde sentido en este caso.

EJEMPLO 1   .

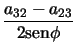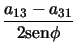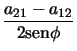
La matriz ortogonal A = 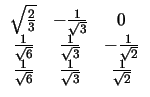$$\left(\vphantom{ \begin{array}{ccc} \phantompar\sqrt{\frac{2}{3}}... ...{6}}}&\frac{1}{{\sqrt{3}}}&\frac{1}{{\sqrt{2}}} \phantompar\end{array} }\right.$$$$\begin{array}{ccc} \par\sqrt{\frac{2}{3}}&-\frac{1}{{\sqrt{3}}}&0... ... \frac{1}{{\sqrt{6}}}&\frac{1}{{\sqrt{3}}}&\frac{1}{{\sqrt{2}}} \par\end{array}$$$$\left.\vphantom{ \begin{array}{ccc} \phantompar\sqrt{\frac{2}{3}}... ...{6}}}&\frac{1}{{\sqrt{3}}}&\frac{1}{{\sqrt{2}}} \phantompar\end{array} }\right)$$ cumple las condiciones del teorema, sus valores propios son $\lambda$ = 1,  $\lambda$ = 0.550477±0.83485 i.  El ángulo de rotación es 1.31812   radianes alrededor de  u = (0.663291, - 0.210819, 0.508961).