|
|
| 1 2 |
|
|
| 1 2 |
Las Calculadoras y el Pensamiento Deductivo
Norma Noguera, Ph. D.
California State University, Long Beach
Long Beach, California 90840
Introducción
Este creciente fracaso que los estudiantes de la escuela media y de secundaria están experimentando en los cursos de matemática, así como el impresionante desarrollo tecnológico de los últimos años han promovido un elevado interés tanto de la sociedad así como de la comunidad educativa en general acerca de la importancia de integrar la tecnología y la enseñanza de la matemática, en los primeros años de la escuela secundaria.
Para lograr un cambio en el currículo de la enseñanza de la matemática es necesaria la creacion de ambientes de aprendizaje que incluyan el uso tecnologías tales como computadoras con el adecuado software y calculadoras con capacidades mayores que las de construir graficos. Ademas es importante considerar un cambio radical en la preparación de los futuros profesores de matemática para que reciban la preparación adecuada para poder implementar en una forma apropiada el uso de estas tecnologías en sus clases con sus futuros estudiantes. Debemos recordar que investigaciones al respecto confirman que los profesores tienden a enseñar en la misma forma en que aprendieron. Otro factor importante es el desarrollo e implementacion de cursos de entrenamiento que incluyan la integración de la tecnología y la matemática para los profesores en servicio De esta manera estos profesores contarian con un medio de actualizar su conocimiento de la materia, y esto tal vez los ayudaria a cambiar sus actitudes hacia la utilizacion de tecnología en el aula.
Objetivo:
El objetivo este estudio es presentar una descripción qualitativa de los resultados obtenidos en una investigación que se realizó con un grupo de estudiantes de 10 año de secundaria (15/16 años). En este estudio se usó la calculadora TI-92 como una herramienta para facilitar el aprendizaje del álgebra.
El objetivo principal de la investigación era observar los (cambios si existían) en el pensamiento lógico deductivo de los estudiantes, así como observar los cambios en sus actitudes y su disposición hacia la matemática cuando usaban la calculadora TI-92 como herramienta para facilitar el aprendizaje.
Poblacion
Se contó con una población de 28 estudiantes matriculados en dos cursos de algebra, que iban a empezar el 10 año y que se encontraban participando en un programa académico de verano en una universidad en el sur de los Estados Unidos. Este programa esta diseñado para ayudar a estos estudiantes a prepararse mejor académicamente para poder ser admitidos en diferentes universidades en los Estados Unidos. Los estudiantes provenían de zonas rurales, eran de escasos recursos económicos y sus padres contaban con escasa educación (ninguno de ellos había terminado la escuela secundaria).
De éstos 28 estudiantes se escogieron seis tomando en cuenta los resultados obtenidos en un examen diagnóstico de actitud hacia la matemática, que se les aplicó a los 28 estudiantes (Ver apendice 1). Los estudiantes escogidos de esta manera fueron mujeres con muy poca experiencia en el uso de cualquir tipo de calculadoras.
Resultados
Todos los lunes y los miércoles durante seis semanas desde las 5:30 p.m. hasta las 8:30 p.m. los estudiantes se reunieron con el profesor investigador el cual usó las primeras sesiones para enseñarlos a usar la calculadora y para reforzar y profundizar los conceptos adquiridos en la clase regular de Algebra. Al mismo tiempo era importante motivar a los estudiantes a ser creativos a la hora de encontrar las soluciones a los problemas. Ademas se les pedia que escribieran los procesos que habian seguido a la hora de resolver el problema.
Durante la primera semana los estudiantes mostraron una actitud muy negativa la cual. se mantuvo hasta la mitad de la segunda semana. Ellos escuchaban las explicaciones del profesor investigador acerca de cómo usar la calculadora, pero no mostraban ningún entusiasmo, interés ni deseo de comunicarse entre ellos ni con el profesor investigador. Se veían inseguros, la calculadora los intimidaba un poco y tenían temor de hacer preguntas. Sin embargo siempre se presentaron a las sesiones y ninguno manifestó deseo de salirse del grupo, a pesar de que ellos sabían que su participación era voluntaria. El profesor investigador realizo muchos intentos durante la primera semana para tratar de motivar a los estudiantes sin lograrlo, sin embargo el miércoles de la segunda semana uno de ellos se atrevió por primera vez a hacer una pregunta, a partir de aquel momento la situación cambió considerablemente, los otros estudiantes empezaron a hacer preguntas y todos empezaron a trabajar como un solo grupo. Se hacían preguntas entre ellos y cada uno aportaba algo a la hora de encontrar las soluciones. Comparaban las respuestas y hacían exploraciones para verificar sus resultados. Ellos mismos construían ejemplos parecidos para facilitar el aprendizaje. El usar la calculadora les permitía hacer los cálculos y los gráficos en minutos evitando así que se sintieran cansados y frustrados cuando cometían un error y tenían que volver a empezar.
Los siguientes son algunos de los ejemplos que los estudiantes resolvieron:
1) Resuelva la siguiente ecuación 3x + 6 = 12. Que sucede con el valor “x” si el coeficiente de x es:
a) Sustituido por su inverso
b) Dividido por 2
c) Multiplicado por 3
2) Resuelva la ecuación 2x2 – 4x + 3 = 0.
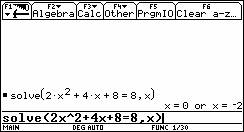
3) Construya el gráfico de
a) Y1 = (x + 6) 2
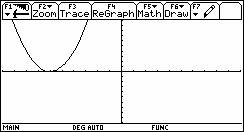
b) Y3 = (x - 2) 2
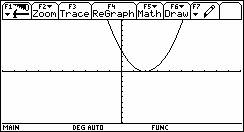
c) Y1 = (x- 5) 2
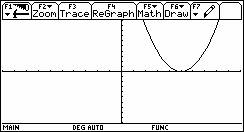
4) Asocie cada función con su gráfico.
a) f(x) = x2 – 4
b) f(x) = -2x2
c) f(x) = (- ½) x2 – 2
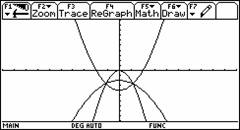
5) Asocie cada función con su gráfico.
1. y = 3x ─ 2
2. y = 2x + 3
3. y = 3x + 7
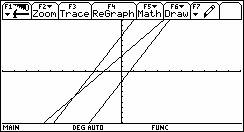
6) Encuentre todos los valores reales de x que satisfacen
2
(2x2 + 8x + 5)(x – 9x + 20) = 1.
Conclusión
La primera semana fue difícil para los estudiantes ya que además de aprender a usar la calculadora tenían que vencer su temor hacia la matemática. Ellos no se mostraban interesados en aprender pero sin embargo no renunciaron a ser parte de la investigación. Cuando se les hacían preguntas respondían diciendo que no sabían. Esta semana fue frustrante y bastante difícil para todos. A mediados de la segunda semana los estudiantes empezaron a cambiar su actitud y empezaron a comunicarse entre ellos. Se hacían preguntas y expresaban lo que no entendían. Al final de las seis semanas fue notorio el cambio que los estudiantes experimentaron especialmente en su forma de razonar al resolver un problema, así como en sus actitudes hacia la matemática. Su confianza y determinación a la hora de resolver un problema fueron evidentes. Usaban diferentes estrategias a la hora de resolver los problemas y su capacidad de deducción fue en aumento. Al final de las seis semanas los estudiantes hicieron una presentación acerca de lo que habían aprendido con la calculadora a toda la clase junto con los profesores directores del programa. Ellos se mostraron muy seguros y demostraron su conocimiento en una forma profesional. Al final de la presentación le manifestaron a las personas presentes que nunca habían soñado con hacer una presentación de matemática al frente de la clase.
1 2