|
|
| Revista Inicio 1 2 3 4 5 6 7 |
La idea de este planteamiento consiste en determinar un método más general, para poder hallar el área de un polígono regular. La forma peculiar de resolución viene dada por la relación:
A = s . a
|
(1) |
Reconociendo el hecho de que todo polígono regular es cíclico (es decir, se puede inscribir en una circunferencia) podemos referirnos a su radio:
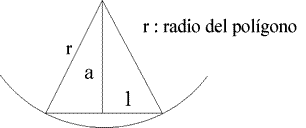
Busquemos una forma alternativa para determinar la apotema a del polígono. El área de la región triangular anterior, se puede determinar de dos formas distintas, a saber:
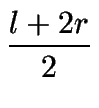
Lo anterior de acuerdo a la forma habitual para hallar el área de un
triángulo y a la relación de Arquímedes.
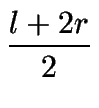 - r - r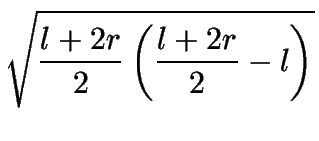 |
|||
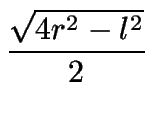 |
En consecuencia en
![]() 1
1![]() tenemos que:
tenemos que:
A = s . 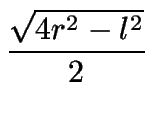 = = |
(2) |
La relación
![]() 2
2![]() es insuficiente en términos
prácticos, pues ésta depende del radio del polígono usualmente
no conocido. Busquemos otra relación más precisa, para ello
consideremos lo siguiente:
es insuficiente en términos
prácticos, pues ésta depende del radio del polígono usualmente
no conocido. Busquemos otra relación más precisa, para ello
consideremos lo siguiente:
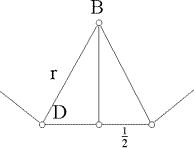
Sabemos que:
B = 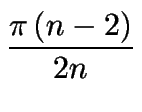 |
(3) |
Por razones trigonométricas:
| cos D | = | 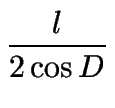 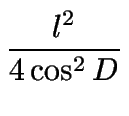 |
|
| = | 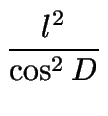 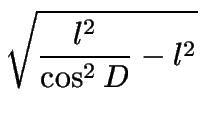 |
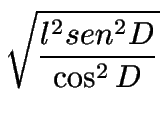 =
= Finalmente el área del polígono regular de n lados, se puede hallar por la relación:
A = 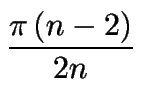 |
(4) |
Es observable de acuerdo a este resultado, que el área de un hexágono regular cuya longitud del lado es l viene dada por:
A = 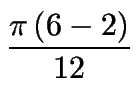 |
(5) |
Una manera muy adecuada y didáctica, para presentar un resultado de este tipo a los estudiantes de secundaria, es utilizar algún software que le permita al estudiante corroborar la relación mediante un laboratorio de verificación. A continuación se expone un laboratorio, basado en el software Sketchpad 3.0.