Herón de Alejandría o el hombre mecánico

Vernor Arguedas T
Escuela de Matemática
Universidad de Costa Rica

	La Dióptra , aparato para medir ángulos y distancias, algo así como un teodolito actual. Lo usó para hacer túneles, mediciones.
	El Odómetro, aparato para contar el número de vueltas de una rueda. Y por la tanto sirve para medir distancias. Es muy probable que la primera de estas máquinas fuera hecha por Arquímedes, durante la primera guerra púnica.
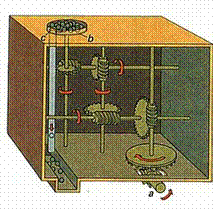
	En esta foto se aprecia el mecanismo por dentro del odómetro
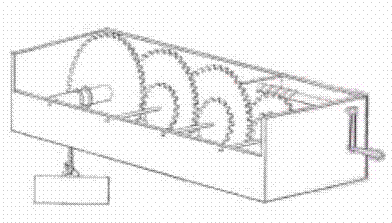
	Barulcos. Aparato para levantar pesos a base de poleas y engranajes
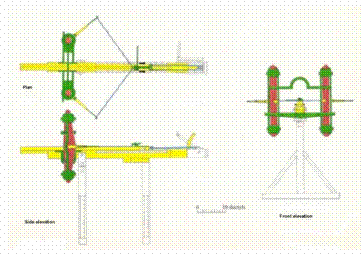
	Quirobalista Aparato para lanzar flechas a larga distancia
	Reconstrucción que ofrece el  Marsden.
	Los autómatas de Heron fueron bien conocidos. Esta reconstrucción de Hércules y el Dragón corresponde a Giovanni Battista Aleoti, 1589, Cuando Hércules golpea la cabeza del dragón, este arroja agua sobre su cara.
	La primera máquina de vapor conocida: la aeolipile

Muchas de las obras de Herón se perdieron ,algunas o fragmentos de ellos se salvaron gracias a las traducciones al árabe. Como muchas veces lo hemos indicado gran parte de nuestra cultura existe gracias al aporte árabe.

•Autómata (Se conserva gracias a una traducción al árabe) (autómata: lo que se mueve por si mismo). Se trata de una colección de construcciones para templos llamadas milagros (thaumata) .Herón muestra puertas que se abren automáticamente, producción de ruidos como truenos, Philon de Bizancio describe algunos autómatas en su libro Mechaniki syntaxis, el cual incluye aparatos astronómicos automáticos alrededor del 300 a.c.

•Dioptra (Traducción al árabe) Se trata de una colección de construcciones para determinar distancias, medir ángulos. Además de la dioptra, aparece el odómetro. En esta obra también analiza problemas de óptica, por ejemplo en la proposición 4 indica: que la luz se mueve siguiendo la trayectoria más corta. Euclides en su óptica afirmó que la luz se mueve en línea recta. Una edición de este texto es:
HERO ALEXANDRINUS. Opera quae supersunt omnia. Vol III: rationes dimetiendi et commentatio dioptrica. Rec. H. SCHOENE. Stuttgart, Tbn., 1976. XXI,366 p. Cl. (BT)(t. & tr.; repr. ed. 1903)

•Métrica (Traducción al árabe) Una colección de 13 libros, para la determinación de áreas y volúmenes, La parte I trata área e triángulos, y polígonos de 4 a 12 lados. Además superficie lateral de pirámides, cilindros, esferas, La parte 2 se refiere al cálculo de volúmenes del cilindro, la esfera, prismas, pirámides, etc., La parte 3 considera la división de áreas y volúmenes en partes. Da un método para el cálculo de la raíz cúbica y calcula la raíz cúbica de 100. – Arquímedes también presenta un cálculo de esta raíz- En esta obra aparece la fórmula de Herón para el cálculo del área del triángulo, conociendo la longitud de sus lados. También aparece un algoritmo para el cálculo de la raíz cuadrada Este algoritmo guarda un cierto parecido al del método de Newton. Además se encuentra por primera vez la referencia a raíces cuadradas de números negativos, al tratar de calcular un frustum imposible de una pirámide La referencia a este libro cuya reaparición es tardía ( redescubierto por R Schoene en 1896, quien recobró en Estanbul -antigua Constantinopla- una copia hecha alrededor del 1100 d.c ) es: 
HERO ALEXANDRINUS. Metrica. Accedunt partes quaedam selectae codicis Constantinopolitani palatii veteris no. 1. Ed. E.M. BRUINS. Leiden, Brill, 1964. 96 p.; 21 figs, 2 tables, 4 pls. Wrs. (Ex libris). 

•Neumática: Una colección de más de 100 aparatos mecánicos que trabajan cono, vapor o presión hidráulica. Incluye entre otras cosas un aparato para extinguir incendios, un aparato que da agua después de introducirle una moneda, la primera máquina de vapor: la aeolipile, además aparecen: la bola de Herón, un termoscopio, un sifón, y una fuente.

•Belopoeica: Una colección de máquinas de Guerra, el manuscrito original se perdió, sin embargo existen algunas transcripciones medievales hechas a mano.

 
•Mecánica: Una colección de 3 libros sobre como mover y levantar objetos pesados
Tal vez estos libros también fueron escritos por Herón.

•Geométrica: Una colección de ecuaciones y ejercicios basados en el primer capítulo de Métrica.

•Estereométrica: Como su nombre lo indica una serie de ejercicios en el espacio basados en el segundo capítulo de Métrica .

•Mediciones: Objetos que pueden ser usados para mediciones basado en Estereométrica y Métrica .Una edición de estos dos textos es la siguiente:
HERO ALEXANDRINUS. Opera quae supersunt omnia. Vol V: Heronis quae feruntur stereometrica et de mensuris. Ed. J.L. HEIBERG. Stuttgart, Tbn., 1976. CXXVI,275 p. Cl. (BT)(t. & tr.; repr. ed. 1914) .

•Quirobalista: Una parte de una colección de catapultas y otros aparatos para lanzar flechas.

•Escolios de Euclides (citados por Proclo)

•Catóptrica: Trata de los espejos planos, cóncavos y convexos. (Esta obra fué atribuída durante bastante tiempo a Ptolomeo).

En la excelente revista electrónica española Gacetilla Matemática http://www.arrakis.es/~mcj/ index.htm , que recomiendo que lean, se presenta la demostración de Herón sobre su fórmula , la cual me permito transcribir:

Determinación del Área de un Triángulo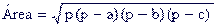   

Posiblemente la expresión matemática más conocida de Herón sea su fórmula para determinar el área de un triágulo conocidos sus lados. Algo realmente útil en aquellos tiempos. Si bien parece que era conocida por Arquímedes, la primera demostración que nos ha llegado figura en la Métrica. El teorema nos garantiza, conociendo las lados de un triángulo, conocer su área, mediante la expresión 

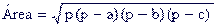
donde a, b y c son los lados del triángulo y p la mitad del perímetro del mismo. 
Aunque ya conocemos una demostración de este teorema en Calculando el área de un triángulo, seguiremos ahora, con la notación actual, el camino que siguió Herón para llegar a dicha expresión. ¡Verdadero encaje de bolillo.! 

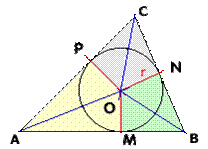	En primer lugar inscribió un círculo en el triángulo y dedujo que el área del mismo era A = r.p (siendo r el radio del círculo y p la mitad del perímetro del triángulo). Como la demostración es, esencialmente, la misma que figura en Calculando el área de un triángulo, la omitimos.  A continuación estudia los triángulos que se forman y llega a la conclusión de que son  congruentes las siguientes parejas de triángulos:  AOM y AOP, BON y CON, AOP y COP  por lo que resulta: AM = AP, BM = BN, CP = CN y además  ángulo (AOM) = ángulo (AOP) ángulo (BOM) = ángulo (BON) ángulo (COP) = ángulo (CON)
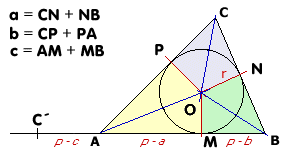
Está clara la intención de Herón al intentar tener sobre la recta base del triángulo la longitud del semiperímetro. No sólo eso, sino que sobre la misma base determina p - a, p - b y p - c, con lo cuál tiene sobre dicho segmento todos los elementos que intervienen en la fórmula. ¡Genial! ... pero aún falta mucho ...	Seguidamente prolongó la base AB hasta C' de forma que AC'= PC (= CN) y argumentó  BC' = BM + MA + AC'= BM + MA + CN =  = 1/2 ( 2 BM + 2 MA + 2 CN) =  = 1/2 ( (BM + AM) + (AM + AP) + (CN + CP) ) =  = 1/2 ( (BM + AM) + (BN + NC) + (AP + PC) ) =  = 1/2 (a + b + c ) = p (semiperímetro)  p - c = (C'A + AM + MB) - (AM + MB) = C'A  p - b = (C'A + AM + MB) - (CP + PA) =  (C'A + AM + MB) - (C'A + AM) = MB  p - a = (C'A + AM + MB) - (CN + NB) =  (C'A + AM + MB) - (C'A + MB) = AM
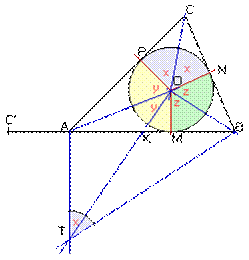
(Reconozco que cuando llegué aquí la primera vez que seguí esta demostración estaba perdido.)	(Reconozco que cuando llegué aquí la primera vez que seguí esta demostración estaba perdido.)  En este momento de la demostración, Herón traza una perpendicular a la base por A y otra al segmento OB (por O). Ambas se cortan en T y une dicho punto con B. Obtiene de esta forma un cuadrilátero TAOB tal que sus ángulos opuestos suman dos rectos (Euclides III.22: " Los ángulos opuestos de los cuadriláteros en los círculos son iguales a dos rectos". El cuadrilátero dado se puede inscribir en un círculo por ser TO perpendicular a OL y AT perpendicular a AB. ¿Cuál es el centro de dicho círculo?); es decir ATB + AOB = 180°.  Como 2x + 2y + 2z = 360° resulta que x + y + z = 180°; puesto que y + z = AOB resulta que x + AOB = 180° = ATB + AOB y concluye que ATB = x.