|
El año en que se demostró la conjetura de Poincaré
Vernor Arguedas T.
Palabras clave: historia, conjetura de Poincaré.
En matemática las conjeturas juegan un papel importante, como también preguntas tales como: ¿qué pasa sí cambiamos esta hipótesis o ¿es este el resultado más general ?. Las preguntas sobre los diferentes temas es esencial para avanzar en en nuestra ciencia. El arte de conjeturar y preguntar debe fomentarse, es uno de los pilares del pensamiento creativo. Junto a las conjeturas, las hipótesis, las paradojas, las generalizaciones, nos encontramos con una larga lista de ejemplos y contraejemplos. Para la escuela
pitagórica todos los números –en nuestro lenguaje-eran racionales.
Conmensurables usaban ellos. Pero, siempre hay un pero, apareció un número
no conmensurable muy sencillo,
Estos números irracionales eran un verdadero dolor de cabeza. El siglo XIX y parte de los inicios del XX vivió esta novela matemática. Algunos hechos sorprendentes para la época fueros los siguientes: había más números irracionales que racionales. Con Lebesgue y su teoría fundamental de la medida, se llegó a otro resultado, los números racionales tienen medida de Lebesgue cero. Cuando surgieron conceptos topológicos, los números racionales tuvieron un papel esencial en el desarrollo. Constituían un conjunto denso numerable de los números reales. Este principio
tan sencillos condujo a un paradoja matemática, monumental en la época,
quizá comparable con la existencia de
No era posible ”construir” a los números reales a partir de los racionales, esto enfrentó a dos titanes, gigantes de la matemáticas: Dedekind y Cantor, pero eso será otra historia. Los pleitos entre matemáticos y matemáticos han sido muy abundantes y en ocasiones han propiciado grandes avances y a veces cotilleos que perduran a través de los años, los lustros y a veces centurias. Sin embargo la densidad de los números racionales en los números reales, condujo a un método de “ construcción matemático” vigente en nuestros días: la completización vía sucesiones de Cauchy. Para Cauchy todas las funciones continuas eran uniformemente continuas, hasta que aparecieron los contraejemplos y un teorema clásico en la enseñanza básica del análisis:
Si
En el siglo XIX había una creencia popular, una conjetura en nuestro lenguaje: toda función continua definida sobre un intervalo tiene puntos en que es derivable. Pero llegó Karl Weierstrass en 1872 y presentó su famoso ejemplo de una función continua no derivable en ningún punto:
Hermite y si discípulo Poincaré, consideraron este ejemplo de Weierstrass, deplorable una cosa infernal. Hermite consideraba estos ejemplos una plaga mortal y su discípulo Poincaré, decía algo como:
No se puede olvidar que Weierstrass era alemán y Hermite y Poincaré eran franceses y que estos dos pueblos han tenidos más de una guerra y disputas de todo tipo. Sin quererlo Weierstrass, había descubierto una mina riquísima: los fractales, su ejemplo es el primero conocido de un fractal y da origen a un método –que se investiga hoy en día-. Por cierto cuando este señor tenía 70 años descubrió su célebre teorema de que toda función continua sobre un intervalo cerrado y acotado es el límite uniforme de polinomios. Poincaré hizo muchos cosas en matemática y su primo en política francesa. Nuestro objetivo, no es hablar de la obra de Poncaré en este artículo sino de su conjetura. En nuestro lenguaje actual la conjetura de Poincaré se podría enunciar como; Si una variedad 3-dimensional compacta sin frontera es simplemente conexa entonces existe un homeomorfismo entre la variedad y la esfera de dimensión 3. Para los estudiantes de matemática y matemáticos en: http://www.4shared.com/account/file.jsp?id=16541682&sId=4VQOqc1gAU6fm43H
recopilé abundantes materiales sobre este tema. En el caso que la liga no funcione seleccione "poincare" en la opción de búsqueda. La conjetura de Poincaré es uno de los problemas del milenium del Clay Mathematical Institute dotado de un premio de un millón de dólares. En http://www.claymath.org/millennium-problems se pueden consultar los 7 problemas. En agosto del 2006 se le concedió la medalla Fields a Grigori Perelman , matemático ruso de San Petesburgo por sus contribuciones a la geometría y su gran creatividad analítica para entender los flujos de Ricci. En otras palabras había resulto en afirmativo la conjetura de Poincaré. Pero siempre hay un pero, Grischa no aceptó el premio y no viajó a España- Antes de Grischa, varios matemáticos chinos habían afirmado que ellos habían resuelto la conjetura antes de Perelman. Sylvia Nasar entrevistó a Perelman –la única entrevista conocida- y escribió un artículo en el The Newyorker por el cual fue demandada por Shing-Tung Yau por considerar que dañaba su imagen. El artículo se puede leer en línea en http://www.newyorker.com/archive/2006/08/28/060828fa_fact2 y se llama "Manifold Destiny". Podríamos decir "el destino de la variedad". El prof Shing-Tung Yau ganó la medalla Fields en 1982 por sus extraorinarios aportes en ecuaciones diferenciales parciales y la conjetura de Calaba en geometría algebraica entre otras cosas. En http://www.doctoryau.com/9.18.06.pdf se puede leer la queja del prof Yau contra Sylvia Nasar y su colaborador.
Cidse -
Revista virtual Matemática, Educación e Internet -
ITCR
|
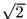 para
los pitagóricos.
para
los pitagóricos.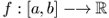 es
continua entonces f es
uniformemente continua. Cuando apareció el concepto de conjunto compacto el
teorema anterior se generalizó como : una función continua con valores
reales definida sobre un conjunto compacto es uniformemente continua.
es
continua entonces f es
uniformemente continua. Cuando apareció el concepto de conjunto compacto el
teorema anterior se generalizó como : una función continua con valores
reales definida sobre un conjunto compacto es uniformemente continua.