┐Cómo plantear y resolver problemas?
José Rosales Ortega
Escuela de Matemática
Instituto Tecnológico de Costa Rica
Resumen:
Todo profesor a nivel universitario y algunos a nivel de secundaria enfrentamos muchas preguntas de nuestros estudiantes, y hasta de nuestros propios colegas. Para muchas de esas preguntas siempre tenemos una respuesta, aunque no siempre sea la mejor. Particularmente,
siempre me han intrigado la siguientes preguntas:
- Cómo se resuelve este problema?
- Cómo asimilar este teorema?
- Cómo se demuestra este teorema?
Algunos eminentes matemáticos tales como G. Polya y J. Dixmier, entre otros, han sugerido algunos lineamientos para ayudar a responder las preguntas anteriores.
La sugerencias de G. Polya para responder a la pregunta de cómo plantear y resolver problemas? son las siguientes:
- Comprender el problema
- Cuál es la incógnita? Cuáles son los datos?
- Cuál es la condición? Es la solución suficiente para determinar la incógnita? Es insuficiente? Redundante? Contradictoria?
- Concebir un plan
- Se ha encontrado con un problema semejante? O ha visto el mismo problema planteado en forma ligeramente diferente?
- Conoce un probema relacionado con éste? Conoce algún teorema que le pueda ser útil? Mire atentamente la incógnita y trate de recordar un problema que le sea familiar y que tenga la misma incógnita o una incógnita similar.
- He aquí un problema relacionado con el suyo y que se ha resuelto ya. Podría usted utilizarlo? Podría emplear su método? Le haría a usted falta introducir algún elemento auxiliar a fin de utilizarlo?
- Podría enunciar el problema en otra forma? Podría planteralo en forma diferente nuevamente?
- Si no puede resolver el problema propuesto, trate de resolver primero algún problema similar. Podría imaginarse un problema análogo un tanto más accesible? Un problema más general? Un problem más particular? Un problema análogo? Puede resolver una parte del problema? Considere sólo una parte de la condición; descarte la otra parte; en qué medida la incógnita queda ahora determinada? En que forma puede variar? Puede usted deducir algún elemento útil de los datos? Puede pensar en algunos otros datos apropiados para determinar la incógnita? Puede cambiar la incógnita o los datos, o ambos si es necesario, de tal forma que la nueva incógnita y los nuevos datos estén más cercanos entre sí?
- Ha empleado todos los datos? Ha empleado toda la condición? Ha considerado usted todas las nociones esenciales concernientes al problema?
- Ejecución del plan
- Al ejecutar su plan de la solución, compruebe cada uno de los pasos.
- Puede usted ver claramente que el paso es correcto? Puede usted demostrarlo?
- Examinar la solución obtenida
- Puede usted verificar el resultado? Puede verificar el razonamiento?
- Puede obtener el resultado en forma diferente? Puede verlo de golpe? Puede usted emplear el resultado o el método en algún problema?
Jacques Dixmier comenta que una de las principales preguntas planteadas muchas veces(con toda razón) por los principiantes es la siguiente: cómo asimilar un teorema? . Al igual que Polya, Dixmier ofrece una respuesta a esta pregunta. El sugiere el siguiente método de trabajo:
- Se lee primero palabra por palabra el enunciado y la demostración, esforzándose por comprender las cadenas lógicas, sin buscar demasiado la idea general. Se puede uno ayudar con diagramas o figuras abstractas.
- Se rehace la demostración en una hoja aparte o en una pizarra, prescindiendo en lo posible del libro.
- Particularizando los datos del enunciado, se examinan casos concretos del teorema. Si es posible, inténtese considerar como casos particulares teoremas ya conocidos.
- El enunciado comprende varias hipótesis; se procura entender la necesidad de todas ellas, suprimiendo para ello alguna de las hipótesis e intentando hallar un ejemplo en el que la conclusión no sea exacta.
- Se buscan generalizaciones del teorema.
- En la demostración hay razonamientos rutinarios y una pequeña cantidad de ideas nuevas; se intentará descubrir estas últimas, de manera que lo esencial de la demostración se resuma en pocas palabras.
- Se vuelve sobre el teorema algún tiempo después, con preferencia la primera vez que se utilice aquel a lo largo del curso.
Este método de trabajo lleva mucho tiempo, y el estudiante no podrá a menudo seguirlo hasta el final. Se le aconseja, sin embargo, que intente la experiencia de cuando en cuando. (Y además, que no se descorazone! Un matemático profesional, reflexionando por centésima vez sobre un teorema sencillo tiene muchas veces la impresión de que ha progresado en la compresnción del mismo, y que su anterior conocimiento era imperfecto.)
Si nos detenemos por un momento a analizar los métodos de trabajo sugeridos por Polya y Dixmier nos percataremos que ambos son extensos y extenuantes. Sin embargo, la experiencia nos demuestra que son muy efectivos.
Ahora que están de moda los concursos de Olimpiadas matemáticas han salido a luz una gran cantidad de libros que se basan exclusivamente en dar sugerencias para resolver problemas. Todas esta sugerencias son en el fondo leves modificaciones de los métodos de Polya y Dixmier. Por ejemplo, el matemático Loren Larson en su libro titulado: ``Problem-Solving Through Problems" sugiere que para resolver problemas matemáticos se debe tener en cuenta lo siguiente:
- Buscar un patrón.
- Hacer figuras.
- Formular un problema equivalente.
- Modificar el problema.
- Escoger una notación adecuada.
- Explotar la simetría.
- Dividir en casos.
- Trabajar hacia atrás.
- Argumentar por contradicción.
- Considerar casos extremos.
- Generalizar.
Se podrían seguir enumerando los métodos de trabajo sugeridos por muchos más notables matemáticos, pero casi todos ellos concuerdan con los de Polya y Dixmier. Últimamente ha surgido la idea que para desarrollar el pensamiento creativo en los estudiantes es muy útil la motivación, una selección apropiada de sugerencias y sobre todo un trato individual a cada estudiantes. En lo que sigue veremos algunos problemas a los cuales les aplicaremos, hasta donde sea posible, los métodos antes expuestos.
- Ejemplo 1
- Los números positivos x, y y z satisfacen
Encuentre el valor de
xy + 2yz + 3zx.
Lo que la mayoría de los estudiantes harían para resolver este problema es tratar de despejar los valores de x, y y z de las ecuaciones del sistema y sustituirla en la expresión
xy + 2yz + 3zx, pero esto no ayuda mucho. Se le suplica al lector que intente este camino para que se confirme nuestra afirmación.
Sin embargo, si tratamos de pensar en algún problema parecido o en algún resultado ya conocido, notaremos que los valores de los lados derechos de las ecuaciones del sistema forman un triple pitagórico, es decir que
25 = 9 + 16. Por lo tanto nuestro problema tiene que ver con el triángulo rectángulo de lados 3, 4 y 5.
Si usamos la siguiente figura
el sistema original adquiere la siguiente forma:
Asumiendo que (ABC) representa el área del triángulo
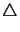 ABC, obtenemos que
ABC, obtenemos que
(ABM) + (ACM) + (BCM) = (ABC).
Por otra parte, se puede observar que
| (ABM) |
= |
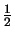 xzsen 120o = xzsen 120o = 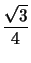 xz xz |
|
| (ACM) |
= |
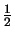 x x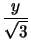 sen 150o = sen 150o = 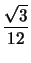 xy xy |
|
| (BCM) |
= |
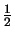 z z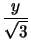 = = 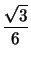 yz yz |
|
| (ABC) |
= |
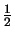 . 3 . 4 = 6. . 3 . 4 = 6. |
|
De esto se puede concluir que
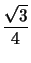 xz + xz + 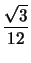 xy + xy + 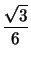 yz yz |
= |
6 |
|
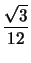 (xy + 2yz + 3xz) (xy + 2yz + 3xz) |
= |
6 |
|
Por lo tanto,
xy + 2
yz + 3
zx = 24
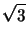
.
- Problema 2
- Sean a, b, c, d números reales en el intervalo
[-
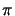 /2,
/2,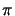 /2], tales que
/2], tales que
-
sen a + sen b + sen c + sen d = 1.
-
cos2a + cos2b + cos2c + cos2d
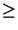 10/3.
10/3.
Demuestre que
a, b, c, d 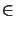 [0,
[0,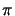 /6].
/6].
Hagamos el siguiente cambio de variables
x = sen a, y = sen b, z = sen c, w = sen d.
De la muy conocida fórmula
cos2a = 1 - 2 sen 2a, se sigue que
cos2a = 1 - 2x2. De la misma forma se obtienen expresiones similares para los otros términos. Sustituyendo en el sistema original, obtenemos que
-
x + y + z + w = 1.
-
x2 + y2 + z2 + w2
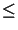 1/3,
1/3,
donde
x, y, z, w 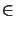 [- 1, 1].
[- 1, 1].
Lo que se debe mostrar es que
x, y, z, w 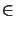 [0, 1/2].
[0, 1/2].
Por el momento supondremos que ya hemos demostrado que nuestros números son no negativos, entonces restaría ver que ellos son menores que 1/2. En efecto, si hacemos los cambios de variables siguientes
| x1 |
= |
1/2 - x |
|
| y1 |
= |
1/2 - y |
|
| z1 |
= |
1/2 - z |
|
| w1 |
= |
1/2 - w, |
|
obtendremos, después de un corto cálculo, que
-
x1 + y1 + z1 + w1 = 1.
-
x12 + y12 + z12 + w12
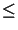 1/3,
1/3,
Por lo tanto, se concluye que
x1 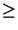 0 y de esto que
x
0 y de esto que
x 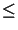 1/2. De igual forma obtenemos que y
1/2. De igual forma obtenemos que y 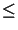 1/2,
z
1/2,
z 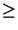 1/2 y
w
1/2 y
w 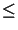 1/2.
1/2.
- Problema 3
- Suponga que n es un número positivo impar. Suponga que escribimos sobre la pizarra los números
1, 2, 3,..., 2n. Elijamos dos números de esa lista, por ejemplo a y b, y borremóslos, luego sustituya los números por | a - b|. Pruebe que al final obtendremos un número impar.
Este es uno de esos problemas que se resuelven por medio de la llamada ``invariancia", es decir que para resolverlo debemos buscar una propiedad que se mantenga invariante a lo largo del proceso que estamos haciendo.
Supongamos que S es la suma de todos los números que están sobre la pizarra. Inicialmente se tiene que
S = 1 + 2 + 3 +
... + 2
n =
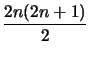
=
n(2
n + 1).
Observe que S es un número impar y además que en cada etapa S se reduce en la cantidad
a +
b - |
a -
b| = 2
. 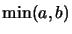
,
el cual es un número par. De esto se sigue que la paridad de S es un invariante, es decir que S se mantiene siempre impar en cada etapa. Por lo tanto el último número que obtendremos será impar.
Queremos terminar expresando que esperamos que este trabajo ayude a obtener una pista de cómo se puede hacer para reolver y plantear problemas matemáticos, muchos de ellos llenos de una belleza genuina. Muchas veces tal belleza es obviada por la mayoría de los estudiantes, ya que como dijo el gran escritor argentino Ernesto Sábato: ``Recobrar la capacidad de asombro"
Revista digital Matemática, Educación e Internet.
Derechos Reservados

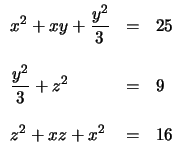
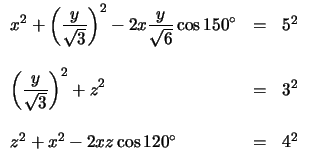
![]() ABC, obtenemos que
ABC, obtenemos que
![]() [0, 1/2].
[0, 1/2].
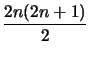 = n(2n + 1).
= n(2n + 1).