-
Notación Funcional, Algunas
Consideraciones
Pedro Díaz Navarro
Escuela de Matemática
Universidad de Costa Rica
El concepto de función es uno de los conceptos matemáticos más
importantes de la matemática moderna. Gracias a este, la matemática
del siglo XX ha alcanzado un grado de abstracción y formalidad sin
precedentes.
La utilidad de las funciones es tal que prácticamente en cualquier
campo de las ciencias exactas, la ingeniería, la economía, la
computación, etc. su conocimiento es, no solo obligatorio sino
indispensable.
Es por esta versatilidad, aplicabilidad e importancia que dicho
concepto se incluye los planes y programas de la enseñanza
secundaria.
Sin embargo, la precisión en la definición que se necesita para
definirla y el nivel de abstracción necesaria por parte de los
educandos para comprenderlo plantea algunos problemas de tipo metodológico
que, si no se consideran, podrían no solo causar una deformación en
el estudiante, con la consecuente apatía de su aprendizaje, sino que
en algunos casos podría inducir a errores teóricos de consideración.
Cuando presentamos la teoría de funciones a nivel de enseñanza
secundaria es común establecer la definición de función de la
siguiente forma:
(De Función) Una Función f de un conjunto A
en un conjunto B es una ley o criterio que asocia a cada
elemento del conjunto A un único elemento del conjunto B2.
El conjunto A se llama Dominio de la función f y
el conjunto B se llama Codominio de la función f.
Los elementos del Dominio se llaman preimágenes y los
elementos del codominio que tienen asociada una preimagen se llaman imágenes.
Al conjunto de imágenes se le llama Ambito de la función f.
La definición anterior se podría presentar separando los
conceptos que la integran para hacerla más comprensible al
estudiante. Esto dependerá de la metodología usada por el educador,
pero en esencia sea cual sea la metodología usada, los componentes de
su definición deben ser al menos los mismos de la definición
anterior.
De la misma definición de función se infiere que una buena técnica
didáctica para su enseñanza será aquella en la que se traten el
concepto de manera integral, dándole igual importancia a los
conceptos componentes involucrados a saber: criterio, dominio,
codominio y ámbito. El descuido de alguno de ellos en el plan de
lección generará ambigüedades que tarde o temprano inducirán a
error como veremos en las siguientes secciones.
Por último indicamos que en la exposición siguiente se asume que
las funciones involucradas son funciones reales de variable real.
Una vez establecida la definición de función se procede a
establecer la notación que convencionalmente se usa para representar
una función a saber:
Denotamos una función f de un conjunto A en un
conjunto B de la siguiente manera:
f : A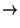 B B; x
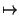 f
f ( x)
Esta notación establece que la función f debe estar
definida de forma que las preimágenes deben pertenecer al conjunto A
y se le deben asociar como imágenes, elementos del conjunto B
por medio del criterio f.
Es común que en el plan de lección se le dé una gran importancia
a la interpretación de esta simbología en lo referente al dominio,
codominio y ámbito de la función f y muy poca o ninguna al
papel que juega el criterio de asociación dentro de esta simbología.
Este es en si un error de consideración por cuanto el abuso de la
notación induce generalmente un error en la evaluación de la función.
Cuando solicitamos calcular
cos(3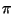 )
dentro de una expresión que involucra varias operaciones , es muy común
omitir los paréntesis y escribir únicamente cos 3 )
dentro de una expresión que involucra varias operaciones , es muy común
omitir los paréntesis y escribir únicamente cos 3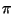 .
Esta forma de escribir es errónea por cuanto induce fácilmente a
error. Ilustramos la situación con el siguiente ejemplo: .
Esta forma de escribir es errónea por cuanto induce fácilmente a
error. Ilustramos la situación con el siguiente ejemplo:
``Calcule
cos 3 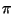
+ 4''
- Si se supone que la función cos(x) se debe evaluar en 3
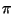 entonces la solución sería 3.
entonces la solución sería 3.
- Si se supone que la función cos(x) se debe evaluar en 3
dejando por fuera a
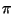 ,
la solución sería
4.88984685 aproximadamente. ,
la solución sería
4.88984685 aproximadamente.
Cuál es la interpretación correcta?
Para una persona con experiencia en la teoría de funciones que ya
conoce los convencionalismos utilizados para evitar el uso
excesivo de paréntesis en las expresiones, puede que la falta de paréntesis
en el ejemplo anterior no le cause problema. Sin embargo, si tomamos
en cuenta que para una primera exposición del tema a estudiantes de
secundaria, la evaluación en funciones es un tema de difícil
comprensión y en este caso el uso de paréntesis es indispensable. El
lector puede comprobar por medio de una calculadora que en el ejemplo
anterior la interpretación correcta es la segunda!!
La ambigüedad y el error del ejemplo anterior radica en el hecho
de que para evitar el uso de paréntesis se ``supone
convencionalmente'' que la función cos(x) se debe evaluar en
la expresión situada inmediatamente a la derecha de la expresión cos
que contenga una variable x o que dependa de ella. El error se
produce por cuanto se ha pasado por alto el hecho de que una función
es un concepto de evaluación uniparamétrico cuando se omiten
los paréntesis. Esto quiere decir que si no se hace el uso adecuado
de paréntesis, cualquier función empleada se evaluará en la primera
cantidad que encuentre inmediatamente después de ella y dejará por
fuera lo demás.
De esta manera, las cantidades:
cos 3 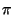
y cos (3 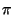 )
representan cantidades diferentes.
De hecho la simbología empleada es bastante clara en la necesidad
del uso de paréntesis. Si pensamos por un momento que la simbología
matemática busca entre otras cosas la claridad de conceptos evitando
símbolos superfluos que oscurecen su significado, vemos que la notación
f (x)
como evaluación de la preimagen (parámetro) x en la función f
debe ser realizado única y exclusivamente en el valor x. Si se
eliminan los paréntesis y se escribe fx se entenderá que el
criterio f se aplicará solo al valor x situado
inmediatamente después. ln x + 4 debe interpretarse de
forma tal que se calcule el valor de ln x y luego al
resultado sumarle 4. Si lo que se desea es calcular el logaritmo
natural de x + 4, entonces debe hacerse uso de los respectivos
paréntesis y escribir
ln(x + 4). Análogamente, si se tiene ln 4x la
interpretación correcta debe ser calcular primero ln 4 y al
resultado multiplicarlo por x. De hecho, el lector puede
observar que no se ``ve igual'' escribir
ln 4x = x ln 4 y
ln x4 = 4 ln x !!. Por otro lado, si lo que se
desea es evaluar 4x en el logaritmo, entonces es necesario el
uso de paréntesis y escribir ln(4x) para evitar la ambigüedad
anterior.
En la sección anterior vimos ejemplos en los que el uso (o no uso) de
paréntesis en la evaluación de una función, induce por lo general a
error. En esta sección veremos algunos ejemplos adicionales del cálculo
superior donde se aprecian los errores que se pueden cometer por falta de
una notación clara originada por el abuso del lenguaje matemático. Además,
se analizan errores inducidos al no tomar en cuenta la definición exacta
y completa de función. Iniciamos nuestro estudio con el siguiente
ejemplo: Durante la aplicación de un examen de cálculo3
se propuso un ejercicio similar al siguiente:
Derive ln xy = 4 donde y = f
(x).
El proposito del evaluador era evaluar la derivación implícita
aplicada a la función ln(xy) de forma que, usando regla de la
cadena, derivara el logaritmo y se calculara y' derivando el
producto xy y despejando y'. O bien separar el logaritmo en
una suma
ln x + ln y y aplicar la derivación implícita a
ln y. Sin embargo, durante la calificación del mismo se
comprobó que algunos estudiantes interpretaron el ejercicio de la
siguiente manera:
ln xy = 4 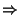 y
y = 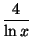
y calcularon y' sin usar derivación implícita!!
El lector podría pensar que la interpretación de los estudiantes es
incorrecta ya que ``en el contexto'' el estudiante debe entender que se
trata de ln(xy) debido a ``la convención'' usada. Si se hubiese
querido la otra interpretación se hubiese escrito y ln x.
Sin embargo, si dicha ``convención'' no se aclara al inicio del curso,
la interpretación hecha por los estudiantes es perfectamente válida. Si
no fuera así, entonces porqué cuando nos encontramos frente a una
expresión de la forma
ln x tan x
automáticamente interpretamos, ``gracias a la convención usada'' ,
ln(x) . tan(x) en vez de
ln(x tan x)? Qué es lo que hace diferente la expresión
ln xy con y = f (x) de la expresión
ln x tan x que permita ``gracias a la convención
usada'', interpretarla de forma diferente? Induce o no induce a error la
convención usada?
Se deja al lector que busque el mismo la respuesta a las primeras dos
preguntas las cuales esperamos pueda encontrar después de leer el
presente artículo. La respuesta a la última de estas preguntas la
responderemos en la siguiente sección.
Una ambigüedad similar se podría dar en el siguiente ejemplo:
Calcule el dominio máximo de la función
f (x) = ln(x2)
Observe que , x2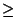 0 y ln(x) tiene dominio
]0,
0 y ln(x) tiene dominio
]0,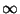 [.
Luego el dominio máximo será
R - {0} . [.
Luego el dominio máximo será
R - {0} .
Supongamos por un momento que omitimos los paréntesis y escribimos
f (x) = ln x2. Entonces se
``podría interpretar'' de la siguiente manera: Como
x2 = x . x se tendría
ln x2 = ln x . x
y como la multiplicación es commutativa se tendría
ln x2 = ln x . x = x
ln x
y como ln x tiene dominio
]0,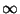 [,
deducimos que el dominio de ln x2 es también
]0, [,
deducimos que el dominio de ln x2 es también
]0,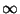 [!!
Es esto correcto? [!!
Es esto correcto?
La respuesta a la pregunta anterior no es clara, si ``la convención
usada'' para evitar el uso de paréntesis no se ha hecho de forma que no
deje lugar a interpretaciones como la anterior se puede penalizar una
solución como la anterior?
Otro tipo de error que se comete en forma muy frecuente es el de no
analizar correctamente una función por evitar el análisis inicial del
dominio máximo de la función. El ejemplo siguiente ilustra esta situación:
Consideremos la función
f (x) = ln(x2) del ejemplo anterior. Su
dominio máximo es como vimos 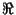 - {0} . Sin embargo, si aplicamos leyes de logaritmos ``podemos escribir
''
- {0} . Sin embargo, si aplicamos leyes de logaritmos ``podemos escribir
''
f (x) = ln(x2) = 2 ln x
Solo que la segunda expresión tiene dominio máximo
]0,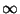 [.
Cómo se explica esto? [.
Cómo se explica esto?
Antes de responder la pregunta del ejemplo anterior veamos otro
ejemplo sobre el mismo tema:
Grafique la función
f (x) = 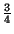 (x2
- 1)2x/3 (x2
- 1)2x/3
Note que para graficar la función anterior debemos analizar primero
el dominio máximo de la función pero si escribimos :
f (x) = 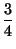 (x2
- 1)2x/3 = (x2
- 1)2x/3 = 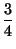 ((x2
- 1)1/3)2x ((x2
- 1)1/3)2x |
(1) |
el lector podrá corroborar con ayuda de un graficador que el gráfico
obtenido será diferente del que se obtiene si escribimos f (x)
de la forma:
f (x) = 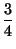 (x2
- 1)2x/3 = (x2
- 1)2x/3 = 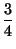 ((x2
- 1)2)x/3 ((x2
- 1)2)x/3 |
(2) |
entonces, cúal es el dominio?
En el ejemplo 5, la función
f (x) = ln(x2) tiene como dominio máximo
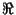 - {0}. Al aplicar las propiedades de logaritmo no tomamos en cuenta de
que este proceso solo se puede aplicar en la intersección de los
dominios de las funciones ln(x2) y 2 ln(x) que
es
]0,
- {0}. Al aplicar las propiedades de logaritmo no tomamos en cuenta de
que este proceso solo se puede aplicar en la intersección de los
dominios de las funciones ln(x2) y 2 ln(x) que
es
]0,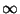 [
por lo que , si se consideran ambas funciones definidas sobre los
dominios máximos respectivos se obtienen dos funciones diferentes en
virtud de la definición de función dada al inicio ya que los dominios
de ambas son diferentes. Luego la igualdad
ln(x2) = 2 ln(x) no es válida como igualdad
funcional salvo que se especifique que ambas funciones están definidas
en el mismo dominio. [
por lo que , si se consideran ambas funciones definidas sobre los
dominios máximos respectivos se obtienen dos funciones diferentes en
virtud de la definición de función dada al inicio ya que los dominios
de ambas son diferentes. Luego la igualdad
ln(x2) = 2 ln(x) no es válida como igualdad
funcional salvo que se especifique que ambas funciones están definidas
en el mismo dominio.
Análogamente, en el ejemplo 6 las manipulaciones algebraicas hechas
en las ecuaciones (1) y (2) cambian los dominios de definición de la
función original y por tanto las segundas igualdades no son válidas
como igualdades funcionales salvo que se especifique que se realicen en
un dominio común. En este caso particular la ambigüedad deriva del
hecho de que la función
xp/q se define como
xpx/q : = e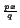 ln(x) ln(x)
de donde vemos la necesidad de evaluar en x > 0. La
composición con x2 - 1 y las posteriores
manipulaciones algebraicas cambian radicalmente el dominio de definición.
Los ejemplos anteriores nos ponen en claro la necesidad de establecer
la convención a usarse en la evaluación de funciones para evitar el uso
de paréntesis o bien no necesitar especificar el dominio de las
funciones estudiadas. El problema esencial de esto es que los libros de
texto empleados a nivel de secundaria no establecen esta convención y
dejan que el estudiante vaya adquiriendo la destreza del no uso de paréntesis
por su propia cuenta lo cual es a fin de cuenta inadecuado.
Por otra parte, el educador debe conocer al menos las reglas básicas
empleadas en la convención usada de lo contrario estará sujeto a
incurrir en situaciones como las anteriormente mencionadas.
De esta manera, y con el fin de dar algún tipo de directriz
establecemos las siguientes reglas que son en general de aceptación
universal:
- En esencia, toda función
f :
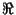 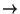 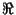 ; x ; x
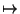 f (x) se evalúa de forma uniparámetrica. Esto es, se
evaluará en el primer valor que encuentre inmediatamente después de
su invocación.
f (x) se evalúa de forma uniparámetrica. Esto es, se
evaluará en el primer valor que encuentre inmediatamente después de
su invocación.
- Si una función f debe ser evaluada en un producto de la
forma
ag(x), a
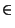
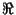 ,
h(x)g(x), o bien en una potencia de la
forma
(g(x))n, n ,
h(x)g(x), o bien en una potencia de la
forma
(g(x))n, n 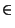
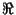 es necesario el uso de paréntesis. De lo contrario se estaría
contradiciendo la uniparametricidad de la evaluación funcional.
es necesario el uso de paréntesis. De lo contrario se estaría
contradiciendo la uniparametricidad de la evaluación funcional.
- Cuando se altere el criterio de una función por medio de alguna
regla algebraica válida en
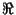 ,
debe indicarse necesariamente el dominio o la restricción respectiva
que esta generando dicho cambio. ,
debe indicarse necesariamente el dominio o la restricción respectiva
que esta generando dicho cambio.
- Cuando se necesite indicar un producto de funciones es conveniente
indicar el punto central que indica el producto.
- El uso de las reglas anteriores o bien de cualquier otra convención
que tienda a evitar el uso de paréntesis o el recargo de notación
debe ser indicado en el plan didáctico inmediatamente después de las
definiciones iniciales para evitar las ambigüedades que devengan de
la falta de claridad notacional. En particular:
- Cuando se eliminen los paréntesis en evaluaciones de la forma f
(ax) como en cos 3x se debe indicar al
estudiante como debe guiarse en la evaluación ya sea que
interprete ``la cercanía'' del evaluando a la función.
- Cuando después de una evaluación de la forma f (ax)
donde se han suprimido los paréntesis aparezca una suma o resta
como por ejemplo
cos 3x + 4, se debe indicar al estudiante como
proceder. Lo más indicado sería el uso de paréntesis.
- Cuando aparezca un producto de funciones de la forma f (x)g(x)
en el cual se han suprimido los paréntesis es necesario indicar
la forma de interpretarlo, ya sea colocando un punto central o
bien separando suficientemente ambas funciones de forma que se
``vea'' que se trata de evaluaciones de x en funciones
diferentes por ejemplo
ln(x)tan(x) = ln x . tan x
o bien
ln(x)tan(x) = ln x tan x
. Lógicamente se debe aclarar esta convención.
- Dado el carácter ``convencional'' de la notación usada, es
necesario indicarle al estudiante que dicha convención puede
variar de un texto a otro por lo que es necesario revisar la
notación usada en los libros de referencia usados.
La definición de función requiere de mucha precisión en su
exposición con el fin de lograr una comprensión adecuada del concepto.
La evaluación de expresiones algebraicas en una función esta muchas
veces sujeta a la determinación de las restricciones que genere dicha
evaluación así como de las manipulaciones algebraicas de que sea objeto
el criterio de la función.
Por otro lado, el desarrollo histórico de la simbología matemática
y los ejemplos anteriormente mencionados, deja en evidencia que el uso de
paréntesis, para indicar el evaluando en una función, no es en general
un recargo innecesario de la notación, sino más bien una necesidad que
evite el uso de convenciones que oscurescan el concepto.
Al lector podría parecerle de poca importancia el hacer énfasis en
el uso de las convenciones notacionales cuando se habla de funciones ya
que si tiene alguna experiencia en la aplicación de funciones, le pueda
parecer que las convenciones se aprenden ``con la práctica'', sin
embargo es necesario aclarar que para una exposición del tema a un nivel
elemental de secundaria, donde los educandos conocen por primera vez el
concepto de función, el desarrollo didáctico y metodológico del tema
debe ser tal que no deje lugar a ambiguedades que puedan inducir a error
al estudiante y lo que es peor le generen una deformación en su aprendizaje
matemático. De hecho, entre menos convenciones se usen más universal
será el concepto y el aprendizaje logrado.
El motivo principal para escribir estas notas fue el observar en la práctica
como se cometen los errores mencionados en los ejemplos anteriores por
parte de los estudiantes e incluso, en algunos casos, por los mismos
profesores. Al notar que el aprendizaje del concepto de función a nivel
de secundaria es en general difícil para el educando y que dicho
concepto juega un rol fundamental en los cursos de nivel universitario
que posteriormente debe llevar, se hace patente la necesidad de generar
una dinámica que tienda a despejar cualquier tipo de duda en torno a
este concepto tanto para los estudiantes como para los profesores que lo
imparten.
[1] Castellón Manuel y otros.
 Tercera Edición. Lehman Editores.
San Jose, Costa Rica. 1980. Tercera Edición. Lehman Editores.
San Jose, Costa Rica. 1980.
[2] Chaverri y otros.
 Litografía Ambar. San Jose Costa
Rica. Litografía Ambar. San Jose Costa
Rica.
[3] Larson y otros .
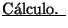 Quinta Edición. Mcgraw Hill. Mexico 1995.
Quinta Edición. Mcgraw Hill. Mexico 1995.
[4] Meneses, Roxana
 .
Grupo Editorial Norma. San Jose Costa Rica. 1991. .
Grupo Editorial Norma. San Jose Costa Rica. 1991.
[5] Rees, Paul y otros.
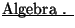 Décima
Edición. Mc Graw Hill. Mexico 1991. Décima
Edición. Mc Graw Hill. Mexico 1991.
[6] Stewart, James .
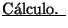 . Tercera Edición. Thompson editores. Mexico, 1998. -
. Tercera Edición. Thompson editores. Mexico, 1998. -
[7] Zill, Denis y otros.
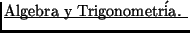 Segunda Edición. Mcgraw Hill.
Bogotá, Colombia. 1992. Segunda Edición. Mcgraw Hill.
Bogotá, Colombia. 1992.
Este documento fue generado usando LaTeX2HTML
translator Version 99.2beta6 (1.42)
|
