Final Olimpiada Matemática Nacional
Examen segundo día
Ciclo A
- 4.
- Se van a escribir números enteros en forma sucesiva y
partiendo de uno hasta que se hayan usado un millón de unos.
Determinar la suma de las cifras del último número escrito
según la secuencia indicada.
- 5.
- Usando los enteros del 1 al 25 sin repetir ninguno,
complete el cuadrado mágico de manera que cada fila, cada
columna y cada diagonal sumen lo mismo.
| 11 |
24 |
|
|
3 |
| |
|
25 |
8 |
|
| |
5 |
13 |
|
|
| |
|
|
14 |
22 |
| 23 |
6 |
|
2 |
|
- 6.
- Sea
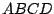 un pentágono regular tal que la estrella
formada por los segmentos
un pentágono regular tal que la estrella
formada por los segmentos 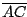 ,
, 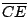 ,
,
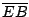 ,
, 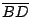 y
y 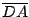 tiene
área 1. Sea
tiene
área 1. Sea 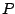 la intersección entre
la intersección entre 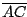 y
y 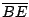 ,
, 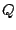 la intersección entre
la intersección entre 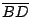 y
y 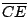 ,
, 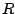 la intersección de
la intersección de 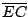 y
y 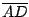 y
y 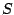 la intersección de
la intersección de 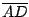 y
y 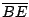 .
.
Determinar el área de la región 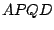 .
.
Ciclo B
- 4.
- Demostrar que en cualquier conjunto de 6 personas
se puede siempre encontrar uno de los siguientes casos:
- Existen tres personas que se conocen entre sí
- Existen tres personas de manera que ninguna
conoce a las otras dos
- 5.
- Encuentre la suma de todos los valores de
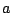 y
y 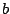 enteros positivos, que cumplan
enteros positivos, que cumplan 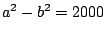 .
.
- 6.
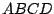 es un trapecio con
es un trapecio con 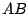 paralelo a
paralelo a 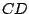 .
Las bisectrices exteriores de los ángulos
.
Las bisectrices exteriores de los ángulos 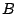 y
y 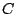 se intersecan en
se intersecan en 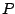 . Las bisectrices exteriores de los
ángulos
. Las bisectrices exteriores de los
ángulos 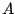 y
y 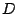 se intersecan en
se intersecan en 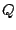 . Demuestre que
la longitud de
. Demuestre que
la longitud de 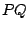 es igual a la mitad del perímetro
del trapecio
es igual a la mitad del perímetro
del trapecio 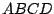 (figura 1).
(figura 1).
Figura 1:
Trapecio 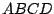 .
.
|
|
Ciclo C
- 4.
- El rectángulo
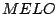 es tal que
es tal que 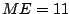 y
y 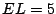 .
Un triángulo
.
Un triángulo 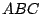 es tal que la intersección de sus
alturas es
es tal que la intersección de sus
alturas es 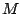 , el centro de su círculo circunscrito es
, el centro de su círculo circunscrito es
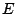 ,
, 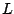 es el punto medio de
es el punto medio de 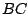 y
y 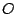 es el pie de la altura
desde
es el pie de la altura
desde 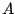 . Determine la longitud
. Determine la longitud 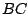 .
.
- 5.
- Se dice que una recta
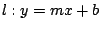 aparta máximamente
a una función
aparta máximamente
a una función 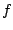 en un punto
en un punto 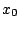 si la gráfica de
si la gráfica de 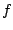 tiene en común con
tiene en común con 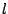 el punto
el punto 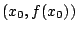 , y además
para todo
, y además
para todo 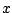 en el dominio de
en el dominio de 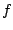 se cumple
se cumple 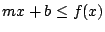 .
.
Para 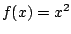 sean
sean 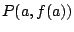 ,
, 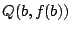 y
y 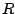 la intersección
de las rectas que apartan máximamente a
la intersección
de las rectas que apartan máximamente a 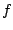 por
por 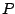 y
y 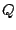 .
Determine el área del
.
Determine el área del 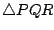 en términos de
en términos de 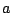 y
y 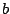 .
.
- 6.
- Sobre un número natural
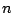 llamaremos la
generalización de
llamaremos la
generalización de 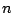 al conjunto que se obtiene del
siguiente proceso: SE ESCRIBE EL NÚMERO EN CUALQUIER
BASE Y SE OBTIENEN TODOS LOS NÚMEROS QUE RESULTEN DE
PERMUTAR ESOS D´IGITOS PARA TODA BASE MENOR QUE
al conjunto que se obtiene del
siguiente proceso: SE ESCRIBE EL NÚMERO EN CUALQUIER
BASE Y SE OBTIENEN TODOS LOS NÚMEROS QUE RESULTEN DE
PERMUTAR ESOS D´IGITOS PARA TODA BASE MENOR QUE 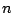 .
.
Demuestre que si 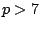 , alguno de los números en la
generalización de
, alguno de los números en la
generalización de 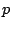 no es primo.
no es primo.
1 2 3
Revista digital Matemática, Educación e Internet.
Derechos Reservados


![]() .
.
![]() sean
sean ![]() ,
, ![]() y
y ![]() la intersección
de las rectas que apartan máximamente a
la intersección
de las rectas que apartan máximamente a ![]() por
por ![]() y
y ![]() .
Determine el área del
.
Determine el área del ![]() en términos de
en términos de ![]() y
y ![]() .
.
![]() , alguno de los números en la
generalización de
, alguno de los números en la
generalización de ![]() no es primo.
no es primo.