Problemas de Olimpiadas 3

 

1. En un tablero de 8 por 8, se colocan 10 fichas que ocupan, cada una de ellas, una casilla. En cada una de las casillas que tiene una ficha, está escrito un número entre 0 y 8, que es igual a la cantidad de fichas colocadas en las casas vecinas. Las casas vecinas son las que tienen un lado o un vértice en común. Muestre una distribución de fichas, que haga que la suma de los números escritos en el tablero sea el mayor posible.
    

2. Sea I el incentro del triángulo ABC. Una circunferencia inscrita en el triángulo ABC y tangente a los lados BC, CA y AB en los puntos K, L y M respectivamente. La recta que pasa por B, paralela al segmento MK, interseca las rectas LM y LK en los puntos R y S, respectivamente. Pruebe que el ángulo 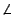$\angle$RIS es agudo.
    

3. Hallar el menor entero positivo n tal que las 73 fracciones
    
   $${\frac{19}{n+21}}$$,$${\frac{20}{n+22}}$$,$${\frac{21}{n+23}}$$,...,$${\frac{91}{n+93}}$$
   sean todas irreducibles.

 

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados