|
Problemas de Olimpiadas
2
- Un recipiente está lleno inicialmente con 16 galones de ácido puro. Se extraen cuatro galones del recipiente y se sustituyen por agua pura. Entonces se sacan nuevamente cuatro galones del recipiente y se vuelven a sustituir por
4 galones de agua. Cuántas veces ha de repetirse el proceso para lograr que la cantidad de ácido en el recipiente sea menos de 1 galón.
- [OIM, 1993 ] Determine todas las funciones de los enteros positivos en si mismos que cumplan las
condiciones:
- f es estrictamente creciente.
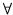 x, y enteros positivos se cumple: x, y enteros positivos se cumple:
f (yf (x)) = x2f (xy)
- Pruebe que si 102 enteros son seleccionados sin repetir del conjunto
{1,2,3,...,200,} entonces entre los números seleccionados hay dos enteros tales que uno divide al otro.
- Sea a un entero positivo impar mayor que 17 de modo que
3a-2 es cuadrado perfecto. Demuestre que existen enteros positivos distintos b y c de modo que a + b, a + c, b + c, y a + b + c son cuadrados perfectos.
|
