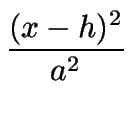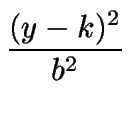1 2 3 4 5 6 7 8 

Patrones y reglas de reescritura

Con la finalidad de presentar un ejemplo de programación simbólica, a continuación se discute el uso de patrones y reglas de reescritura para definir un procedimiento que determina la forma canónica de la ecuación de una sección cónica, a partir de su ecuación polinomial.

La idea general del método es proponer un conjunto de reglas, cuya aplicación permita transformar la ecuación polinómica en dos variables, a la forma canónica de una cónica. Para simplificar el problema sólo se consideran las formas canónicas de elipses e hipérbolas:

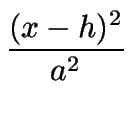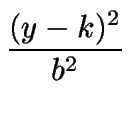$${\frac{(x-h)^2}{a^2}}$$±$${\frac{(y-k)^2}{b^2}}$$ = 1.

Los patrones en Mathematica son expresiones que incluyen el objeto Blank[ ] identificado usualmente con el símbolo de subrayado (_ ), y que representa a cualquier tipo de expresión --cualquier cosa en Mathematica--. Así por ejemplo: x_ es un patrón que se asocia o empata con cualquier expresión y se denomina x, n_Integer es un patrón para una expresión denominada n que tiene cabeza Integer, es decir que es un entero y x_Symbol^2 representa cualquier símbolo elevado al cuadrado.

Descargar FCano.nb

                         

 

Una regla de transformación es una expresión de la forma patrón -> expresión, que utiliza un patrón para establecer la forma de las expresiones a las que se aplicará y una expresión --en términos de los elementos del patrón-- que determina la nueva forma que debe asumir expresión. Para aplicar las reglas se usa el operador /. denominado Replace.

Por ejemplo, en la ilustración anterior, se da una regla para transformar ecuaciones pasando constantes numéricas al lado derecho. En este caso, cuando se aplica la regla a la primera ecuación, el patrón e_ empata con la expresión 2x + x² + y. Y cuando se aplica a la segunda ecuación no se provoca ningún cambio, porque la ecuación no empata con el patrón de la regla -- el lado derecho no es una expresión numérica -- y por lo tanto la transformación no se aplica.

Descargar FCano.nb

                           

 

Con la regla dos se usa el patrón a_. x_Symbol^2 que empata con cualquier producto de una expresión denominada a con un símbolo al cuadrado, por ejemplo 3z². El punto en el patrón se utiliza para que un solo símbolo al cuadrado también empate con el patrón, asumiendo en ese caso que a = 1. Observe que el patrón x_^ 2 puede empatar con expresiones como t², (y - 1)² o (cos(x))², pero x_Symbol^ 2 empata sólo si el término al cuadrado es un símbolo como t², z² o x².

Por otra parte, en la siguiente ilustración, se usa el operador //. -ReplaceAll-, para aplicar las reglas recursivamente hasta que ninguna regla sea aplicable al resultado obtenido.

Descargar FCano.nb

                           

 

La definición de una función en Mathematica, por ejemplo f[x_] := x^2+1, es una regla de transformación global que se aplica en todo lugar donde la expresión f[x] tenga lugar. Así, a continuación se definen dos funciones o reglas de transformación globales, identificadas con el nombre aFormaCanonica. La primera, aFormaCanonica[liz_ == lde_], recibe una ecuación en cualquier forma, pasa a la izquierda su parte derecha, dejando en cero esta última. Luego le aplica las reglas de transformación vistas con anterioridad y que han sido registradas como una lista denominada Reglas. Finalmente se invoca recursivamente a sí misma, pero asegurándose de que el nuevo argumento sea de la forma

ax² + by² = 1,

para que se aplica la segunda regla global para darle finalmente la forma:

$${\frac{x^2}{\alpha^2}}$$ + $${\frac{x^2}{\beta^2}}$$ = 1.

Naturalmente, la regla aFormaCanonica[a_.x_^2 + b_.y_^2 == 1] dada se aplica sólo cuando el argumento sea una ecuación que empate con el patrón dado. Mathematica ordena las reglas globales según su grado de generalidad, de lo particular a lo más general, y se aplican en ese orden.

Descargar FCano.nb

                              

 

Aunque los ejemplos dados tienen un perfil introductorio, todos ellos han querido mostrar que Mathematica provee cantidad de procedimientos para obtener soluciones directas a gran diversidad de problemas matemáticos y de las ciencias en general. Y que el lenguaje para hacerlo es también un lenguaje de programación con enorme potencial. Un lenguaje de programación, que comienza a desbordar los sistema del álgebra simbólica, para encontrar aplicaciones en otros campos de las ciencias de la computación.

1 2 3 4 5 6 7 8

Revista Virtual, Matemática Educación e Internet.
Derechos Reservados.