1 2 3 4 5 6

¿Qué es la División Sintética?

La División Sintética es un procedimiento abreviado para realizar la división de un polinomio P(x) = a_nxⁿ + a_{n - 1}x^{n - 1} +...+ a₁x + a₀ de grado n, esto es a_n $\not=$ 0, entre un polinomio lineal x - c. El procedimiento para realizar esta división es muy simple, primero se toman todos los coeficientes del polinomio P(x) y la constante c, con estos se construye una especie de ''casita'' que ayudará en el proceso

                                                           

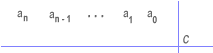
Lo primero es ''bajar'' el coeficiente a_n, a este coeficiente también lo denotamos por b_{n - 1}, luego se multiplica por la constante c, el resultado se coloca en la segunda columna y se suma al siguiente coeficiente a_{n - 1}, al resultado lo denotamos b_{n - 2}

                                                       

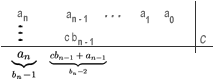
Este último resultado se multiplica nuevamente por c y se le suma al coeficiente a_{n - 2} y el proceso se repite hasta llegar a a₀. Los resultados parciales que se obtienen se denotan por b_{n - 1},  b_{n - 2},   ^... ,  b₁,  b₀ (se inicia con b_{n - 1} pues el cociente tiene un grado menos que el dividendo), y el último valor obtenido se denota por r, pues es el residuo de la división, de esta manera lo que se obtiene es

                                            

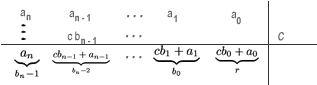
Así, el cociente de la división de P(x) por x - c es b_{n - 1}x^{n - 1} + b_{n - 2}x^{n - 2} + ^... + b₁x¹ + b₀ con un residuo r, en donde los coeficientes se detallan como

b_{n - 1} = a_n

b_{n - 2} = cb_{n - 1} + a_{n - 1}

b_{n - 3} = cb_{n - 2} + a_{n - 2}

$$\vdots$$

b₁ = cb₂ + a₂

b₀ = cb₁ + a₁

r = cb₀ + a₀

EJEMPLO 1 (División Sintética)  
Realice la división de P(x) = 3x⁴ + 2x³ - x² + 4x + 2 entre x + 2.

Solución

Al realizar el algoritmo de la división sintética con los coeficientes de P(x) y -2 como valor de c se obtiene

                                                                

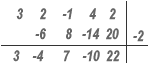
Así, el cociente de la división de P(x) entre x + 2 es 3x³ - 4x² + 7x - 10 y se obtiene un residuo r = 22.

Revista Matemáticas, Educación e Internet^â
Derechos Reservados