![]()
Se tomará el polinomio
P(x) = anxn + an - 1xn - 1 +...+ a1x + a0 y lo vamos a factorizar para expresarlo de forma
''encebollada'', para esto se saca a factor común la variable x y se repite el proceso n - 1 veces, veamos
P(x) = anxn + an - 1xn - 1 +...+ a1x + a0
![]() P(x) = (anxn - 1 + an - 1xn - 2 +...+ a2x + a1)x + a0
P(x) = (anxn - 1 + an - 1xn - 2 +...+ a2x + a1)x + a0
![]() P(x) = ((anxn - 2 + an - 1xn - 3 +...+ a3x + a2)x + a1)x + a0
P(x) = ((anxn - 2 + an - 1xn - 3 +...+ a3x + a2)x + a1)x + a0
![]()
![]() P(x) = (((...(((anx + an - 1)x + an - 2)x + an - 3)x +...+ a3)x + a2)x + a1)x + a0
P(x) = (((...(((anx + an - 1)x + an - 2)x + an - 3)x +...+ a3)x + a2)x + a1)x + a0
Esta manera de expresar al polinomio es la mejor para evaluar los polinomios en programas de computación, en los cursos de algoritmos se encuentra que genera menos errores y es más eficiente. Si se evalúa este polinomio en c se obtiene
P(c) = (((...(((anc + an - 1)c + an - 2)c + an - 3)c +...+ a3)c + a2)c + a1)c + a0
Ahora se verá cómo es que se evalúa al polinomio, se inicia con an, luego se multiplica por c y se le suma an-1, al resultado obtenido anteriormente se le multiplica por c y se le suma an - 2, y así sucesivamente hasta llegar a sumar el valor a0; a estos resultados parciales se les denotará como bn - 1, bn - 2,..., b1, b0 y al último término que se obtiene se denotará como r, se debe observar que este último valor es la evaluación completa del polinomio, por lo que también le llamaremos P(c), así
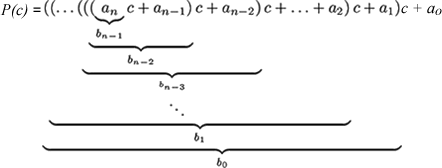
Si se continúa con este proceso hasta llegar a a0 se puede observar que
Si se comparan estos resultados con los coeficientes que se obtienen luego de efectuar el proceso de la división sintética, se observa que son equivalentes, es decir que ¡este es el mismo proceso!, lo interesante es preguntarse ¿por qué esta forma de evaluar el polinomio da los coeficientes del cociente y el residuo si se toman los resultados parciales?
Revista Matemáticas,
Educación e Internetâ
Derechos Reservados