1 2 3 4 5

Punto interior de un triángulo

En muchas tareas de programación de gráficos, se necesita seleccionar y arrastrar un objeto geométrico. Para simplificar la discusión, supongamos que tenemos el siguiente problema: tenemos un triángulo (que se puede deformar arrastrando sus vértices) y queremos trasladarlo arrastrando el ratón sobre él. En el "programita" que sigue abajo, se puede arrastrar el triángulo con el ratón y también se puede deformar el triángulo arrastrando los vértices. Cada vez que hacemos clic dentro de la zona gris se despliega un punto rojo, excepto si hacemos clic en el interior del triángulo.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

Arrastrar el triángulo. Se puede deformar el triángulo arrastrando
sus vértces con el mouse

Para hacer la implementación necesitamos resolver tres problemas

Cómo decidir si el 'ratón' está sobre el triángulo?
Arrastrar el triángulo
Solucionar el problema de refrescamiento de imágenes

Punto interior a un triángulo

Para resolver el problema de decidir si el ratón esta sobre el triángulo, hacemos uso de algunas ideas del Algebra Lineal. Para esto consideremos un ángulo con un vértice v₀, como se muestra en la figura que sigue.

En esta figura, los vectores v₁ y v₂ son los rayos del ángulo con vértice en v₀. Ahora tomamos un punto v y lo expresamos como

v = v₀ + a₁v₁ + a₂v₂

resolviendo para a₁ y a₂ obtenemos

a₁

$\displaystyle {\frac{v \otimes v_2 - v_0 \otimes v_2}{v_1 \otimes v_2}}$

a₂

$\displaystyle {\frac{v \otimes v_1 - v_0 \otimes v_1}{v_1 \otimes v_2}}$

donde u $\bigotimes$ v : = u_xv_y - u_yv_x

Nota: La fórmula definida para vectores en dos dimensiones u $\otimes$ v, es una derivación del cálculo formal
u × v = (u_x, u_y, 0) × (v_x, v_y, 0) = (u_xv_y - u_yv_x)k

Es claro que si a₁ > 0 y si a₂ > 0, entonces v estará en el interior del ángulo con vértice en v₀.

De esta manera, v esta en el interior del triángulo si es interior a cada uno de los tres ángulos del triángulo.

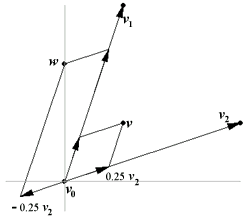
Por ejemplo, consideremos v0 = (0,0), v1 = (1,3) y v2 = (3,1).

Si tomamos v = (1,1) entonces v = v0 + 0.25 v1 + 0.25 v2, así que como a1 = 0.25 > 0 y a2 = 0.25 > 0 entonces v está en el interior del ángulo

Si tomamos w = (0,2) entonces w = v0 + 0.75 v1 - 0.25 v2, así que como a1 = 0.75 > 0 y a2 = - 0.25 < 0 entonces w está fuera del interior del ángulo

Este resultado se puede reformular en términos de orientación de un triángulo. Este otro punto de vista nos permite formular un algoritmo sencillo para resolver el primer problema.

Orientación de tres puntos

Decimos que tres puntos del plano tienen orientación nula si son colineales, en otro caso decimos que tres puntos A1, A2 ,A3 están orientados de manera positiva si para visitar estos tres puntos en el orden dado, nos movemos contra-reloj y que están orientados de manera negativa si para visitar estos tres puntos en el orden dado, nos movemos a favor del reloj.

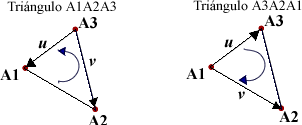
La orientación del triángulo depende del orden en que se especifican
sus vértices, usando el producto cruz u × v podemos calcular la orientación

Con el producto cruz definido en R³ se puede establecer una manera sencilla para determinar la orientación de tres puntos A1, A2, A3 (en este orden). LLamemos u = A1 - A3 y v = A2 - A3 entonces

u × v = (u_x, u_y, 0) × (v_x, v_y, 0) = (u_xv_y - u_yv_x)k

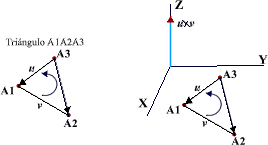
La fórmula que resultó es natural ya que los tres puntos están en el plano XY, por lo tanto el producto cruz es un vector en la dirección del eje Z. Podemos usar el signo de la componente u_xv_y - u_yv_xpara definir la orientación, así si

u $\otimes$ v : = u_xv_y - u_yv_x

entonces, la orientación es positiva si u $\otimes$ v > 0 y la orientación es negativa si u $\otimes$ v < 0

Por ejemplo si A1 = (2,3), A2 = (3,5), A3 = (1,4) entonces

Si u = A1 - A3 y v = A2 - A3 tendríamos u $\otimes$ v = 3 > 0, por tanto la orientación de A1A2A3 es positiva

Si u = A3 - A1 y v = A2 - A1 tendríamos u $\otimes$ v = -3 < 0, por tanto la orientación de A3A2A1 es negativa

Finalmente, decimos que el triángulo $\triangle$ ABC esta orientado positivamente si los vértices A, B, C están, en este orden, orientados positivamente. De manera análoga decimos que el triángulo está orientado negativamente si los vértices A, B, C están, en este orden, orientados negativamente. Así, en el ejemplo anterior, el $\triangle$ A3A2A1 está orientado negativamente.

1 2 3 4 5

Revista Virtual, Matemática Educación e Internet.
Derechos Reservados.