1 2 3 4 5 

 

Punto interior en un triángulo y orientación

Se puede reformular el resultado acerca de los puntos interiores en un triángulo de esta manera

Teorema. Consideremos un triángulo $ \triangle$ABC y un punto P del plano. P está en el interior de este triángulo si la orientación de los triángulos $ \triangle$ABP, $ \triangle$BCP y $ \triangle$CAP es la misma que la orientación del triángulo $ \triangle$ABC.

Aquí hay que recordar que la orientación de cada triángulo se determina de acuerdo a la dirección del movimiento cuando se visitan los vértices  en el orden especificado. Consideremos el triángulo ABC de la figura. El punto Q no está en el triángulo. Esto se puede verificar computacionalmente observando que el triángulo ABQ tiene orientación contraria al triángulo ABC. Los triángulos ABP, CAP,BCP si mantienen la orientación así que se puede establecer computacionalmente que P está en el interior del triángulo.




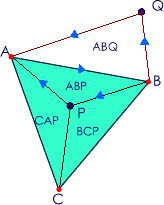
B no es interior al triángulo ABC pues el triángulo  
ABQ tiene orientación contraria al triángulo ABC



En este teorema, la orientación de un triángulo es la misma que la orientación de sus tres vértices, así que podemos establecer un algoritmo sencillo para decidir si un punto está o no en el interior de un triángulo. En efecto, consideremos un triángulo $ \triangle$A1A2A3. Llamemos u = A1 - A3 y v = A2 - A3, entonces el signo de u $ \otimes$ v decide la orientación del triángulo. En el fragmento de código que sigue, a   u $ \otimes$ v se le llama  "areaT"   pues con esta fórmula también se puede calcular el área  del triángulo (en realidad con la norma del producto cruz)

  

     //código Java
 float areaT(Point2D A1,Point2D A2,Point2D A3)
    {//área del triángulo  A1A2A3, es > 0 sii esta orientado positivamente,else < 0
     return (A1.x - A3.x)*(A2.y - A3.y)-(A1.y - A3.y)*(A2.x - A3.x);

    }//

 boolean estaEnTri(Point2D A1,Point2D A2,Point2D A3, Point2D P)
    {   // Decide si un punto P está dentro del triángulo orientado A1A2A3

        if(areaT(A1,A2,A3)>=0)
               return areaT(A1, A2, P) >= 0 &&
                      areaT(A2, A3, P) >= 0 &&
                      areaT(A3, A1, P) >= 0;
        else   return areaT(A1, A2, P) <= 0 &&
                      areaT(A2, A3, P) <= 0 &&
                      areaT(A3, A1, P) <= 0;

    }//

Observemos que  permitimos que AreaT(Ai,Aj,P) sea 0. Con esto dejamos que los puntos de los lados sean también considerados interiores.

En el siguiente "programita", se muestra como trabaja el algoritmo. Al entrar el ratón al triángulo, se muestra un punto amarillo (no hay necesidad de arrastrar el ratón, solo moverlo). El triángulo se puede deformar.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado


En la práctica estos métodos trabajan bien si el próposito es decidir si un punto es interior a un triángulo dado pero eventualmente, con un valor flotante x, podemos considerar reemplazar un test de la forma x $ \geq$ 0 con x $ \geq$ - $ \epsilon$ donde se podrá poner, por ejemplo $ \epsilon$ = 10-6

Arrastrar el triángulo

Para arrastrar el triángulo $ \triangle$A1A2A3 debemos hacer una traslación de los vértices en la dirección del movimiento del ratón. Si llamamos Pini al punto inicial del movimiento (presionamos el botón derecho y arrastramos) y Pactual a cada nuevo punto en el recorrido del ratón mientras es arrastrado, entonces el triángulo $ \triangle$A1A2A3 se debe actualizar como $ \triangle$B1B2B3    con  Bi = Ai  +  Pactual - Pini   como se observa en la figura que sigue.

 

 

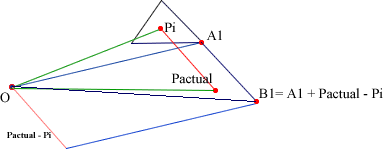
Podemos visualizar esta traslación arrastrando el triángulo en el siguiente "programita". Al arrastrar el ratón se muestra el vector que da la dirección de traslación. Si lo arrastramos sobre el triángulo, se muestra la traslación de los vértices.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

 

 1 2 3 4 5 

Revista Virtual, Matemática Educación e Internet.
Derechos Reservados.