Gráficos Java Swing, Java2D

Método de graficación.

Ahora que podemos leer funciones y evaluarlas, ya podemos implementar el método que construye el gráfico de la función.

> Coordenadas de pantalla y coordenadas reales

Primero debemos establecer un factor de escala para el eje X y el eje Y. Digamos 'escalaX = 30 pixeles' y 'escalaY=30 pixeles'.

Ahora debemos manejar la conversión entre coordenadas en números reales y coordenadas de pantalla. Supongamos que la variable 'aReal' corresponde al valor como número real de la coordenada de pantalla 'a'

Conversión: números reales a coordenadas de pantalla

a = (int)Math.round(escalaX * (aReal ) );

Conversión: coordenadas de pantalla a números reales

aReal = 1.0*a/escalaX;

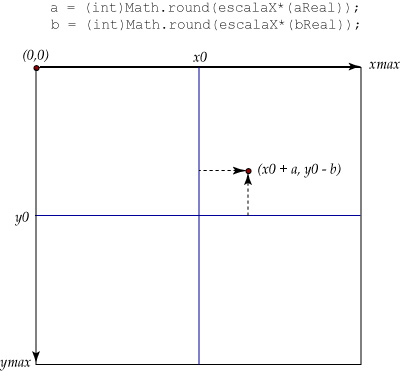
Vamos a suponer que el origen del sistema, en coordenadas de pantalla, es (x0,y0). En la siguiente figura se observa la representación del par ordenado (aReal, bReal) en coordenadas de pantalla (a,b) respecto al origen (x0,y0).

> Métodos de Java2D

Para dibujar el gráfico de la función necesitamos un dominio [xmin, xmax] y un conjunto de pares ordenados 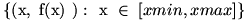en coordenadas de pantalla.

Estos pares ordenados los unimos luego con segmentos de recta. Para crear segmentos y puntos (discos) vamos a usar los métodos gráficos de Java2D. Para esto necesitamos la biblioteca java.awt.geom.*.

Definimos un par de constantes para controlar el grosor (stroke) y las líneas punteadas (dashed)

final static BasicStroke grosor1 = new BasicStroke(1.5f);
final static float dash1[] = {5.0f};
final static BasicStroke dashed = new BasicStroke(1.0f,
                                                  BasicStroke.CAP_BUTT,
                                                  BasicStroke.JOIN_MITER,
                                                  5.0f, dash1, 0.0f);

Para habilitar anti-aliasing se usa el método

setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);

Segmento de (x1, y1) a (x2, y2)

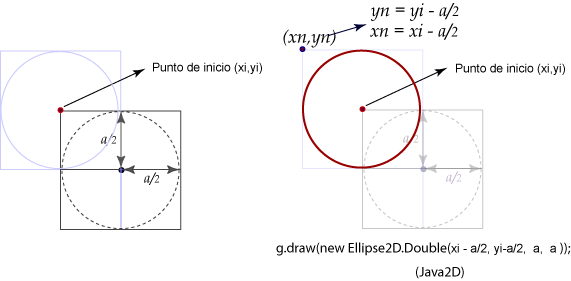
draw(new Line2D.Double(x1,y1,x2,y2));

Círculo con centro en (xi, yi) y radio 'a'

draw(new Ellipse2D.Double(xi-a/2,yi-a/2,a,a));

Dominio de graficación.

En este graficador vamos a graficar en todo el dominio de pantalla, pensando en que más adelante vamos a arrastrar el origen de coordenadas con el mouse. Una vez que hemos elegido el origen de coordenadas (x0,y0) -en coordenadas de pantalla- podemos establecer xmin y xmax como los extremos de la región de graficación y luego pasar estas coordenadas de pantalla a números reales para poder calcular los pares ordenados

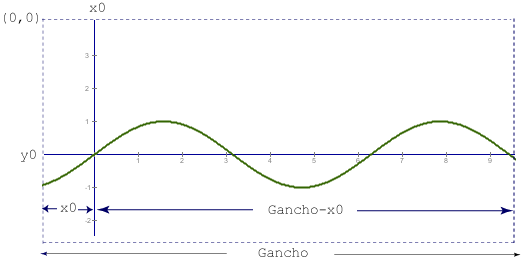
Así, haciendo la conversión a números reales

xmin = -1.0*x0/escalaX;
xmax = (1.0*(Gancho-x0)/escalaX);

Ahora ya podemos crear el método gráfico.

Método 'Graficar'

void Graficar(Graphics ap, int xg, int yg)
{
int xi=0,yi=0,xi1=0,yi1=0,numPuntos=1;
int cxmin,cxmax,cymin,cymax;
double valxi=0.0, valxi1=0.0, valyi=0.0,valyi1=0.0;
Complex valC; //manejo de complejos en JEP
double imgx;

//convertimos el objeto ap en un objeto Graphics2D para usar los métodos Java2D
Graphics2D g = (Graphics2D) ap;
g.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);

g.setFont(ft10);
g.setPaint(new Color(0,0,150));

//eje Y
g.draw(new Line2D.Double(xg, 10, xg, Galto-10));
//eje X
g.draw(new Line2D.Double(10, yg, Gancho-10, yg));

xmin=-1.0*xg/escalaX;
xmax=(1.0*(Gancho-xg)/escalaX);
cxmin=(int)Math.round(xmin); //pantalla
cxmax=(int)Math.round(xmax);
cymin=(int)Math.round(1.0*(yg-Galto)/escalaY);
cymax=(int)Math.round(1.0*yg/escalaY);

numPuntos=Gancho; //num pixels

g.setPaint(Color.gray);
g.setFont(ft7);

//marcas en los ejes (ticks)
if(escalaX>5)
{
    for(int i=cxmin+1;i<cxmax;i++)
    { g.draw(new Line2D.Double(xg+i*escalaX, yg-2, xg+i*escalaX , yg+2));
       if(i>0)
          g.drawString(""+i, xg+i*escalaX-2, yg+12);
       if(i<0)
         g.drawString(""+i, xg+i*escalaX-6, yg+12);
    }
}

if(escalaY>5)
{
    for(int i=cymin+1;i<cymax;i++)
    { g.draw(new Line2D.Double(xg-2, yg-i*escalaY, xg+2 , yg-i*escalaY));
       if(i>0)
          g.drawString(""+i, xg-12,yg-i*escalaY+3 );
       if(i<0)
         g.drawString(""+i, xg-14,yg-i*escalaY+3 );
   }
}
g.setPaint(new Color(50,100,0));

g.setStroke(grosor1);
miEvaluador.parseExpression(Tffun.getText());
errorEnExpresion = miEvaluador.hasError(); //hay error?

if(!errorEnExpresion)
{
    Tffun.setForeground(Color.black);

    for(int i=0;i<numPuntos-1;i++)
    {
      valxi   =xmin +i*1.0/escalaX;
      valxi1 =xmin+(i+1)*1.0/escalaX;
      miEvaluador.addVariable("x", valxi);
      valyi   = miEvaluador.getValue();
      miEvaluador.addVariable("x", valxi1);
      valyi1 = miEvaluador.getValue();
      xi      =(int)Math.round(escalaX*(valxi));
      yi      =(int)Math.round(escalaY*valyi);
      xi1     =(int)Math.round(escalaX*(valxi1));
      yi1     =(int)Math.round(escalaY*valyi1);

     //control de discontinuidades groseras y complejos
      valC = miEvaluador.getComplexValue();
      imgx = (double)Math.abs(valC.im());
     if(dist(valxi,valyi,valxi1,valyi1)< 1000 && imgx==0)
     {
       g.draw(new Line2D.Double(xg+xi,yg-yi,xg+xi1,yg-yi1));
     }
    }//fin del for
}else{mensaje.setText(":. Hay un error.");
        Tffun.setForeground(Color.red);
}
}//

Ahora agregamos este método a al clase interna ZonaGrafica y lo llamamos en paintComponet()

class ZonaGrafica extends JPanel
{
   public void paintComponent(Graphics g)
   {
     super.paintComponent(g);
     Graficar(g, x0, y0);     //x0,y0 se inicalizan en init
     showStatus("https://tecdigital.tec.ac.cr/servicios/revistamatematica/");
   }

   void Graficar(Graphics ap, int xg, int yg)
{
   .....
}

}

Claro, todavía falta agregar en el constructor de ZonaGrafica, los eventos de arrastre del mouse

>>> Inicio 1 2 3 4

Revista digital Matemática, Educación e Internet.
Derechos Reservados