Algunos aspectos
sobre Ecuaciones Funcionales
Josť
Rosales Ortega
Escuela de Matemática
Instituto Tecnológico de Costa Rica
Las ecuaciones funcionales son un tópico muy conocido de las
matemáticas. Por ejemplo, se conoce que las funciones continuas
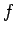 que verifican la ecuación funcional que verifican la ecuación funcional
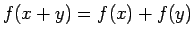 son de
la forma son de
la forma 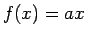 , donde , donde 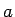 es una constante. De igual forma se
sabe que la función que verifica que es una constante. De igual forma se
sabe que la función que verifica que
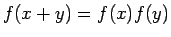 es la
función exponencial. es la
función exponencial.
Una particularidad de las ecuaciones funcionales es que no hay un
método universal para resolverlas. Lo que existe es una guía de
cómo aproximarse a encontrar la solución, en el caso en que
exista.
En esta nota queremos tratar con ecuaciones funcionales del
siguiente tipo
e indicar cómo proceder a la búsqueda de sus soluciones.
- Problema 1
-
- Encontrar todas las funciones
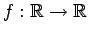 que verifican que verifican
Una idea que siempre está presente en la resolución de
ecuaciones funcionales es la de buscar alguna función que
verifique nuestra ecuación. Es fácil darse cuenta que
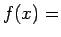 sen sen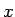 es una solución de la ecuación funcional anterior. Lo
único que debemos hacer es recordar que es una solución de la ecuación funcional anterior. Lo
único que debemos hacer es recordar que
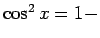 sen sen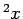 . .
Una vez que tenemos una solución surge de inmediato la pregunta
siguiente: nuestra solución será la única? Algunas veces
sí. Veamos que en nuestro caso la función
sen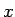 es la
única solución de la ecuación funcional. es la
única solución de la ecuación funcional.
Si deseamos mostrar que nuestra solución es la única que
satisface la ecuación anterior entonces el método de ataque es
el siguiente: supongamos que hay otra función, digamos 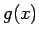 , que
también es solución de la ecuación y tratemos luego de probar
que , que
también es solución de la ecuación y tratemos luego de probar
que 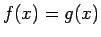 , para todo , para todo
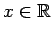 . Esto mostrará la unicidad de
la solución. . Esto mostrará la unicidad de
la solución.
Sea entonces que
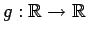 también es solución de
la ecuación funcional (1), es decir que se cumple: también es solución de
la ecuación funcional (1), es decir que se cumple:
Restando (2) de (1), obtenemos
Usando la fórmula para la diferencia de cubos y luego
factorizando, obtenemos que (3) es equivalente a
De lo anterior se sigue que
Y esto último es equivalente a que
Por lo tanto,
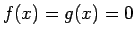 , para todo , para todo 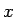 número real. número real.
Lo anterior prueba que
sen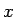 es la única solución. es la única solución.
- Problema 2
-
- Encontrar todas las funciones
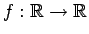 que verifican que verifican
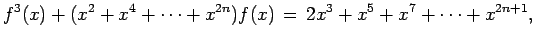  |
(4) |
Procediendo como en el problema anterior vemos que 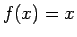 es una
solución de la ecuación funcional (4). Ahora veamos si
tal solución es única. es una
solución de la ecuación funcional (4). Ahora veamos si
tal solución es única.
Igual que antes supongamos que
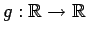 es otra
solución de la ecuación funcional (4), es decir que es otra
solución de la ecuación funcional (4), es decir que
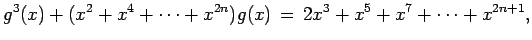  |
(5) |
Si restamos (5) de (4) obtenemos que
luego, usando una vez más la diferencia de cubos y factorizando,
obtenemos que
La idea ahora es observar que los términos
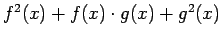 se pueden escribir de la siguiente forma se pueden escribir de la siguiente forma
Usando lo anterior se concluye que
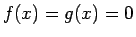 , y con
lo cual se concluye que , y con
lo cual se concluye que
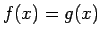 , para todo
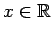 .
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|