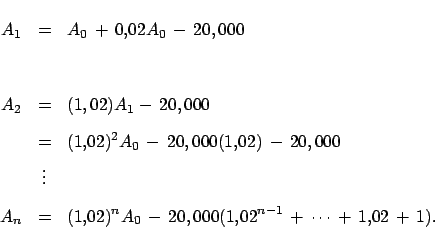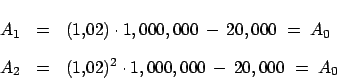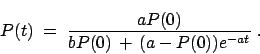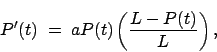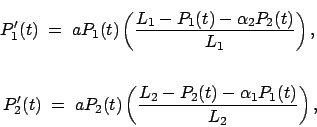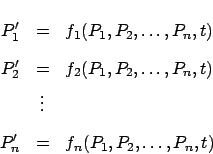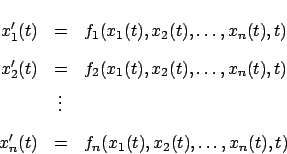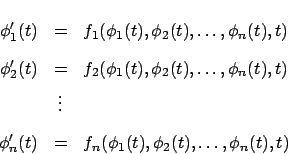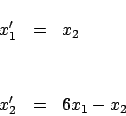Se sabe que ciertas especies animales se multiplican, en condiciones ideales(comida en abundancia, sin luchas internas, etc.), de manera tal que el crecimiento de la población es proporcional a la cantidad de miembros de la especie. Es decir que si
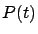
denota la población en el tiempo
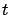
, y
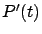
es la velocidad con que varía la población, entonces existe una constante
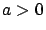
, tal que
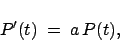 |
(1) |
para todo
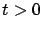
, donde 0 denota el tiempo a partir del cual comenzamos a hacer nuestra observavión, y la constante
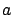
depende de la población en cuestión y del medio ambiente. Esta ecuación es el ejemplo más sencillo e importante de lo que es una ecuación diferencial. Es fácil ver que cualquier función que satisface la ecuación diferencial (
1) necesariamente es de la forma
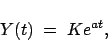 |
(2) |
donde
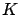
es una constante, determinada por la ``condición inicial". En nuestro caso
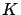
es la población inicial en
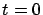
. La ley de crecimiento de la población dada por la ecuación (
1) se conoce como la Ley Malthusiana de crecimiento, y la ecuación (
2) nos dice que si la especie en cuestión se rige por esta ley de crecimiento, entonces, independientemente de la población inicial, si
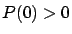
, la población tenderá a infinito exponencialmente. La experiencia nos enseña que esto no sucede en la realidad por tiempo prolongado, así que debe haber otros factores a considerar. Una vez que la población sobrepasa un cierto número, comienza a haber escasez de alimentos, se producen luchas internas, desechos contaminantes, etc. Esto nos lleva a considerar la ``Ley logística" de crecimiento de poblaciones:
donde
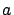
y
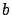
son constantes positivas y
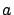
es mucho mayor que
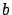
. Las constantes
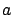
y
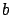
son los
coeficientes vitales
de la especie. Obsérvese que si la población
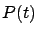
es
``pequeña" , el término
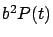
es despreciable, pues
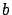
es
muy pequeña en relación a
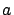
., por lo que el crecimiento
asemeja al regido por la ley malthusiana. Sin embargo, al aumentar
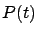
la contribución
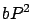
crece en forma cuadrática, por
lo que juega un papel importante.
Esta ecuación diferencial es de primer orden, del tipo ``separable" y por tanto es fácil de resolver; si 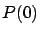 es la población inicial en
es la población inicial en 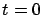 , entonces (por el teorema de existencia y unicidad de soluciones con condiciones iniciales) existe una única función de
, entonces (por el teorema de existencia y unicidad de soluciones con condiciones iniciales) existe una única función de 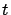 que satisface la ecuación diferencial y toma el valor
que satisface la ecuación diferencial y toma el valor 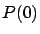 en
en 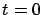 . La solución buscada es
. La solución buscada es
Si hacemos 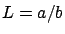 , observamos que
, observamos que 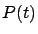 tiende a
tiende a 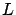 cuando
cuando 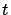 tiende a
tiende a 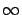 , independientemente de la población inicial, pues
, independientemente de la población inicial, pues 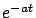 tiende a 0 cuando
tiende a 0 cuando 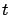 tiende a
tiende a 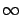 . Además,
. Además, 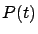 es una función monótona creciente para
es una función monótona creciente para 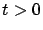 . Más aún, dado que
. Más aún, dado que
se ve que
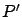
es creciente para
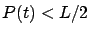
y es
decreciente para
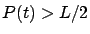
, con un punto de inflexión en
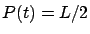
. Por tanto la gráfica de
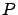
es del tipo:
A partir de esta información concluimos que el período de tiempo antes de que la población alcance la mitad de su límite 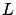 , es un período de crecimiento acelerado, semejante al crecimiento regido por la ley malthusiana. Después de este punto, la tasa de crecimiento disminuye hasta llegar a cero.
, es un período de crecimiento acelerado, semejante al crecimiento regido por la ley malthusiana. Después de este punto, la tasa de crecimiento disminuye hasta llegar a cero.
De esta forma la ley logística nos permite hacer predicciones sobre el crecimiento de las especies, predicciones que se han comprobado en diversos estudios y experimentos.
Observése que la ley logística
puede escribirse en la forma
donde
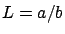
es el límite de la población. El término
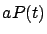
es el potencial biótico de la especie, es decir, la tasa
potencial de crecimiento en condiciones ideales, y el término
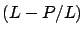
es la resistencia ambiental al crecimiento.
Ahora bien, supongamos que tenemos dos especies 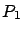 y
y 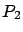 , cuyo crecimiento se rige por la ley logística cuando las especies están aisladas de otras. Qué sucede si ahora juntamos a las especies
, cuyo crecimiento se rige por la ley logística cuando las especies están aisladas de otras. Qué sucede si ahora juntamos a las especies 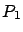 y
y 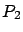 , de manera que tienen que competir entre sí por el alimento, espacio, etc.? En este caso las ecuaciones se transforman en
, de manera que tienen que competir entre sí por el alimento, espacio, etc.? En este caso las ecuaciones se transforman en
donde
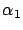
y
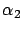
son constantes que indican el grado de influencia de una especie en la otra. Nos interesan preguntas como las siguiente:
- Existen constantes
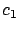 y
y 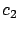 tales que
tales que
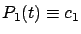 y
y
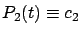 satisfacen el sistema de ecuaciones anterior? Si tales valores existen, se les llama puntos de equilibrio del sistema.
satisfacen el sistema de ecuaciones anterior? Si tales valores existen, se les llama puntos de equilibrio del sistema.
- Supongamos que
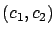 es un punto de equilibrio del sistema, y que súbitamente agregamos algunos miembros de la primera especie, permanecerán
es un punto de equilibrio del sistema, y que súbitamente agregamos algunos miembros de la primera especie, permanecerán 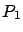 y
y 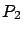 cerca cerca del valor
cerca cerca del valor 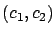 , para todo tiempo futuro? Puede suceder, por ejemplo, que los miembros adicionales de la primera especie le den a ésta una ventaja sobre la segunda especie, de manera que ésta tienda a la extinción, mientras que
, para todo tiempo futuro? Puede suceder, por ejemplo, que los miembros adicionales de la primera especie le den a ésta una ventaja sobre la segunda especie, de manera que ésta tienda a la extinción, mientras que 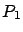 tiende a un valor límite
tiende a un valor límite 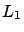 Si esto sucede diremos que el punto
Si esto sucede diremos que el punto 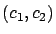 es inestable. Mientras que si
es inestable. Mientras que si 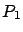 y
y 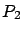 permanecen cerca de
permanecen cerca de 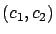 para todo tiempo futuro, diremos que este punto de equilibrio estable. Más aún, puede suceder que si agregamos algunos miembros de cualquiera de las dos especies, al pasar el tiempo las dos poblaciones
para todo tiempo futuro, diremos que este punto de equilibrio estable. Más aún, puede suceder que si agregamos algunos miembros de cualquiera de las dos especies, al pasar el tiempo las dos poblaciones 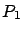 y
y 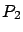 tienden otra vez a la solución de equilibrio
tienden otra vez a la solución de equilibrio 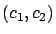 . En este caso se dice que
. En este caso se dice que 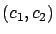 es un atractor.
es un atractor.
- Supongamos que
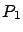 y
y 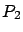 tienen valores arbitrarios para
tienen valores arbitrarios para 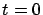 . Qué ocurre cuando el tiempo tiende a infinito? Triunfará alguna de las dos especies, tenderán a una solución de equilibrio?
. Qué ocurre cuando el tiempo tiende a infinito? Triunfará alguna de las dos especies, tenderán a una solución de equilibrio?
Si en vez de dos especies en competencia, consideramos tres especies, o 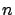 especies en competencia, lo que obtendremos es un sistema de ecuaciones de la forma
especies en competencia, lo que obtendremos es un sistema de ecuaciones de la forma
donde
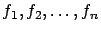
son funciones de
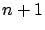
variables. Esto es lo que se concoce como un sistema de
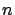
ecuaciones diferenciales de primer orden. A un conjunto de funciones que satisfagan este sistema, se les llama una solución. Parte fundamental de estos sistemas dinámicos es el estudio de las propiedades cualitativas de las soluciones, donde por propiedades cualitativas entenderemos propiedades del tipo de las mencionadas en las preguntas del ejemplo 2.
Dado un sistema de ecuaciones diferenciales
una solución del sistema es un
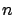
-ada
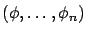
de funciones de
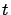
que satisfacen el sistema. Es decir,
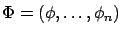
satisface
Por ejemplo, la pareja
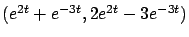
es una solución del sistema lineal de primer orden
Obsérvese que para cada
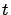
, la
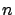
-ada
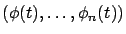
es un punto de
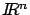
. Así, al variar el tiempo, la solución
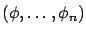
describe una curva, o trayectoria en
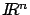
. En este caso a
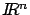
se le llama el espacio fase, y la curva que describe la solución en
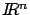
se llama una órbita del sistema. Las soluciones de equilibrio
corresponden al caso donde las derivadas
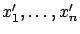
son cero para todo
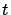
, así que la órbita consiste de solamente un punto en el equilibrio. El teorema fundamental de ecuaciones diferenciales es el teorema de existencia y unicidad de soluciones, el cual nos dice que si las funciones
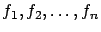
son funciones diferenciables, entonces
- Las órbitas son curvas simples, es decir, sin auto-intersecciones.
- Las órbitas son ajenas dos a dos: si dos órbitas se intersecan en un punto son idénticas. Por cada punto del espacio fase pasa una y solamente una órbita del sistema.
- Las órbitas llenan todo el espacio
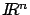 .
.
Luego, dado un sistema de ecuaciones como el anterior, sus órbitas descomponen al espacio fase en unión disjunta de curvas simples y puntos de equilibrio. A esta descomposición de 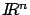 se le conoce como el retrato fase del sistema dinámico. Nos preguntamos cuestiones como: Existen puntos de equilibirio? Cuántos hay? Existen órbitas periódica? Cuáles son los conjuntos límites de esas órbitas?, o en otras palabras, dónde se acumulan o dónde nacen y dónde mueren las órbitas?, etc.
El estudio de estas y otras preguntas relacionadas, constituye el estudio central de los sistemas dinámicos.
se le conoce como el retrato fase del sistema dinámico. Nos preguntamos cuestiones como: Existen puntos de equilibirio? Cuántos hay? Existen órbitas periódica? Cuáles son los conjuntos límites de esas órbitas?, o en otras palabras, dónde se acumulan o dónde nacen y dónde mueren las órbitas?, etc.
El estudio de estas y otras preguntas relacionadas, constituye el estudio central de los sistemas dinámicos.
- M. Braun, (1990) Ecuaciones diferenciales y sus Aplicaciones, Grupo Editorial Iberoamérica, México.
- J. Hale and H.Kocak, (1991) Dynamics and Bifurcations,
Springer-Verlag, New York.
- Morris Hirsch and Stephen Smale, (1983) Ecuaciones diferenciales, sistemas dinámicos y álgebra lineal, Alianza Universidad
Textos, Espa
 a.
a.
- Lawrence Perko, (1991) Differential Equations and Dynamical Systems,
Springer-Verlag, New York.
- José Seade, (1994) Una introducción a los sistemas dinámicos, Ciencia, México, Abril-Junio.