Inicio

Aspectos Técnicos y Metodológicos para el Diseño de Instrumentos Educativos Multimediales de Cálculo Diferencial e Integral

Pedro Díaz Navarro 

Resumen

Se dan técnicas generales para la elaboración de instrumentos didácticos digitales elaborados en MATEMÁTICA 5.0 para los cursos de cálculo diferencial e integral impartidos a las carreras de ingenierías y computación 

Palabras Clave:  MATHEMATICA 5.0, Diseño, Cálculo Diferencial, Cálculo Integral.

Introducción

El Cálculo Diferencial e Integral es una materia indispensable en la formación de los profesionales de las áreas de ciencias exactas, ingenierías y computación. Se puede decir que es el primer curso de nivel Universitario en los planes curriculares de las carreras de Ingeniería Civil, Ingeniería Química, Ingeniería Mecánica, Topografía, Geología, Ciencias de la Computación etc. 

El contenido del curso es esencial para el desarrollo de las demás materias de matemática de estas carreras por lo que el dominio de los temas desarrollados es fundamental.

Recientemente, el desarrollo de software especializado tanto en cálculo diferencial e integral como en otras áreas de la matemática, ha hecho que las distintas facultades de las universidades se interesen por incluir en la descripción curricular de estas materias, el uso de estas plataformas digitales con el fin de “mejorar” el aprovechamiento y la promoción de los cursos.

Sin embargo, esta iniciativa ha encontrado serios obstáculos para su realización. Entre ellos podemos señalar los siguientes:

• Falta de licencias de los programas utilizados.
• Falta de capacitación de los profesores en el uso de algún programa específico.
• Falta de capacitación de los profesores en la didáctica de plataformas multimediales en matemática.
• Falta de capacitación de los profesores en el diseño de instrumentos multimediales en matemática.
• Falta de capacitación de los profesores en el uso de técnicas audiovisuales

Ciertamente, la falta de presupuesto de las escuelas impide adquirir suficientes licencias para crear laboratorios multimedia que permitan el adecuado uso de los programas especializados. Pero más grave aún es la imposibilidad de poder desarrollar un curso de cálculo debido a la falta de profesores capacitados. Este debe ser uno de los primeros recursos con que se debe contar antes de pensar en la elaboración de reformas curriculares que implementen los recursos computacionales en los distintos cursos de matemática ya que de nada vale tener una descripción curricular que incorpore estos aspectos si no se cuenta con un cuerpo docente capacitado para desarrollarlo.

De esta forma, es necesario desarrollar iniciativas que promuevan la actualización en aspectos multimediales de los profesionales de matemática y enseñanza de la matemática y sobre todo en el uso de algunas plataformas especializadas para matemática.

El presente trabajo pretende dar una guía para el profesor de matemática en el manejo de algunos aspectos técnicos multimediales para el desarrollo de instrumentos educativos multimediales para cálculo diferencial e integral. Para esto, se dan lineamientos generales para el diseño y realización de estos y se toma como base el programa MATHEMATICA 5.0 de Wolfram Research para mostrarle al profesor como elaborar presentaciones que ayuden al estudiante a la comprensión de los conceptos básicos de esta materia. 

Las técnicas aquí presentadas podrán, “mutatis mutandis”, ser exportadas a otras plataformas especializadas en matemática. 

Perfil de entrada del estudiante de Cálculo Diferencial e Integral.

El estudiante que matricula un curso de cálculo diferencial e integral debe tener una formación sólida en los conceptos de factorización, racionalización, simplificación y desarrollo de expresiones algebraicas, dominar la técnicas de acotamiento mediante desigualdades y sobre todo dominar la teoría básica de funciones y operaciones con funciones. Con respecto a este último aspecto, debe conocer las funciones elementales básicas estudiadas en secundaria a saber: Función lineal, Función Cuadrática, Funciones Trigonométricas, Funciones Exponencial de base a>0 y Logaritmo de base a>0 y dominar las propiedades básicas de dichas funciones.

Estudios realizados en la Universidad de Costa Rica mediante un examen de diagnostico han determinado que hay una cantidad importante de estudiantes que ingresa a los cursos de cálculo diferencial e integral de las diferentes carreras, que no poseen los conocimientos mínimos básicos para enfrentar dichos cursos. Esto genera una alta deserción inicial por parte de los estudiantes. Aunque no se han realizados estudios completos para determinar la causa de esta deserción, se ha podido detectar algunos aspectos que podrían incidir en el bajo aprovechamiento del curso están relacionados con esta carencia de los fundamentos teóricos requeridos para llevar el curso.
Los aspectos mencionados anteriormente han fundamentado la necesidad de elaborar instrumentos educativos usando programas especializados de matemática y que le ayuden al profesor de matemática a introducirse en el ámbito del desarrollo de los instrumentos educativos digitales.

Diseño de Laboratorios y presentaciones para Cálculo Diferencial e Integral
Con base en lo expresado anteriormente, se tiene que un curso de cálculo diferencial e integral tiene cuatro temas principales: Introducción o repaso de la teoría de funciones, Limites y Continuidad, la Derivada y sus aplicaciones y la Integral y Cálculo de Primitivas. De esta forma es conveniente diseñar los cuatro laboratorios siguientes

• Introducción al programa utilizado y la Teoría Básica de Funciones: En este se debe hacer referencia a la sintaxis básica usada en el programa para realizar las operaciones aritméticas básicas, graficaciones de funciones, resolución de ecuaciones. La práctica de los estudiantes debe ser elaborada de forma que se practique los comandos básicos de cálculos aritméticos, evaluación de expresiones, graficación de funciones en rangos distintos, traslaciones de gráficos etc.

• Cálculo de Límites de funciones: En este módulo, el profesor explicará el concepto de límite mediante tablas de valores, gráficas y animaciones que le permitan al estudiante comprender el concepto de “acercamiento” por la derecha y por la izquierda de la variable independiente hacia un valor dado y el comportamiento de las imágenes para valores cerca del punto hacia el cual tienden las imágenes. Este proceso tiene dos objetivos principales. El primero mostrar el concepto de límite y el de continuidad de una función. El segundo mostrar la sintaxis necesaria de la plataforma usada para que el estudiante pueda elaborar sus propias tablas, gráficas y cálculos de límites. La práctica de laboratorio se desarrollará en función de que el estudiante aprenda a calcular los límites de funciones tanto en un punto como al infinito. Además el estudiante debe elaborar tablas de valores de funciones para “intuir” el comportamiento de la función “cerca del punto al cual se calcula el límite. En la medida que la plataforma lo permita se puede pensar en calcular límites laterales. 

• Cálculo de derivadas: Este módulo tiene por objetivo presentar al estudiante el concepto de recta tangente a la curva en un punto mediante una animación en la que se muestre como una recta secante “tiende” a la recta tangente a la curva en un punto y como a partir de este se obtiene el concepto de Derivada de una función en un punto dado. Además se procede a indicarle al estudiante como hacer el cálculo de derivadas de funciones que normalmente requieren de mucho trabajo por parte del estudiante. Así, se muestra la importancia de la herramienta computacional en los casos donde los cálculos se vuelven muy elaborados. Nuevamente, el objetivo de la práctica será familiarizar al estudiante con la sintaxis básica del programa para el cálculo de derivadas. Para esto, es útil elaborar una lista de funciones para las cuales el cálculo de la derivada sea muy laboriosa.

• Cálculo de Primitivas I Cálculo de Integrales definidas, Métodos Numéricos para el Cálculo de Integrales: En este último módulo de dan los comandos necesarios para el cálculo de primitivas y de integrales definidas. Además en la medida que el programa lo permita es conveniente que se represente el área entre la curva de una función positiva y el eje x, el área entre curvas y el área de funciones generales y se les compare con el valor de la integral. También es útil escoger algunas funciones donde el cálculo de sus primitivas sea difícil para mostrar la utilidad y potencia de la herramienta computacional. Finalmente, se puede hacer una introducción al cálculo aproximado de áreas mediante el método del trapecio o método de Simpson. La práctica para el estudiante estará en función de reforzar estos conceptos.

Es recomendable que dichos laboratorios sean pensados como complemento a las clases magistrales y no como sustituto de ellas. La experiencia indica que si no se aclaran los conceptos matemáticos previos, posiblemente se haga más difícil el aprovechamiento del laboratorio.
También, es recomendable que el profesor realice una presentación previa a cada laboratorio con una duración no mayor de diez minutos donde se muestren los comandos básicos que serán practicados en el laboratorio. Así, todo laboratorio debe tener al menos dos partes: una presentación del profesor y una guía práctica para el estudiante con la que pueda practicar los conceptos 
Y comandos explicados por el profesor. Además el apoyo del profesor durante el desarrollo de la práctica es fundamental para que el estudiante pierda el stress inicial de enfrentarse a la nueva herramienta.
La evaluación de los laboratorios se puede realizar por medio de tareas o una evaluación corta en la que el estudiante demuestre el dominio de la sintaxis de la plataforma utilizada.

Aspectos Técnicos de las presentaciones para Cálculo Diferencial e Integral

El profesor que desarrolle laboratorios y presentaciones multimediales para matemática debe de tener formación en tres aspectos: como especialista en contenidos, como técnico del programa o plataforma usada y como diseñador audiovisual. Comúnmente se tiende a descuidar este último aspecto y se le da énfasis a la parte técnica o al contenido. Sin embargo, los instrumentos que descuiden el manejo de la imagen audiovisual, por lo general tienden a cansar al publico hacia el cual va dirigido.
De esta manera, se recomienda que el especialista en contenido que decida desarrollar material educativo para matemática deberá considerar las siguientes indicaciones:

• El tiempo: Se recomienda que una presentación no dure más de 10 minutos. Si se hacer una presentación muy larga se tiende a disminuir la atención del público meta.

• El Contenido: Se recomienda que en pantalla no aparezca más de seis líneas de texto. El exceso de texto tiende a cansar la vista y por lo general no se lee. 

• La tipografía: El tipo y tamaño de letra debe ser legible. Preferiblemente los tipos Arial o Verdana son adecuados. 

• La cantidad de contenido en pantalla: El exceso de contenido en la pantalla tiende a causar saturación visual lo que ocasiona que el lector se abstenga de leer la información. Se recomienda que se presente la cantidad mínima de texto o simbología y que sea el orador el que explique la información presentada.

• El color: La letra negra y el color blanco es adecuada para el texto escrito, sin embargo para una presentación con proyector no es recomendable pues tiende a cansar la vista. Se recomienda que el fondo de la presentación sea un color azul o negro y que el color de la letra o simbología se escoja por contraste. Además es conveniente resaltar con otro color, los conceptos más importantes de la presentación. En todo caso, se debe tener en cuenta que el uso de color no debe causar saturación o ambigüedad visual. 

• El audio: Cuando sea pertinente, el apoyo de algún efecto de sonido puede ser una valiosa herramienta sobre todo si se trata de captar la atención del público. Sin embargo, este recurso no debe convertirse en un pretexto para mostrar las habilidades del expositor en el uso de la herramienta. 

• La oralidad: El discurso del profesor es fundamental. Es conveniente que el profesor explique ampliamente los conceptos que se muestran en pantalla y que a su vez complemente la exposición. También se recomienda que la presentación no se convierta en un monologo sino que las dudas tanto teóricas (relativas a la materia) como técnicas (relativas al software) se vayan aclarando conforme se desarrolla la presentación. 

Laboratorios con MATHEMATICA 5.0 para Cálculo Diferencial e Integral

Las técnicas de diseño presentadas en la sección anterior se pueden aplicar, en general, a cualquier tipo de programa. El diseñador de instrumentos educativos multimediales en matemática debe de tener un conocimiento general de estos. 
Para mostrar su aplicación recurriremos a el programa MATHEMATICA 5.0 es cual una plataforma especializada para el cálculo matemático de altísima precisión. De hecho, los cálculos se realizan en forma simbólica y en aritmética de punto flotante las aproximaciones se pueden realizar con tantos decimales como se desee. 
El programa posee un conjunto de comandos y bibliotecas que permiten realizar gráficas en dos y tres dimensiones. Además se pueden desarrollar animaciones que permitan visualizar eventos matemáticos trascendentales en el aspecto didáctico.
Específicamente, el programa puede ser usado para desarrollar “notebooks” que le permitan al estudiante repasar los conceptos estudiados en cálculo diferencial e integral y además le permita al estudiante revisar los resultados de sus cálculos. 
Por ejemplo, el siguiente código muestra como hacer una animación en MATHEMATICA 5.0 en la cual se muestra el concepto de límite.
Primeramente cargamos una biblioteca para hacer gráficos mediante el comando siguiente:

(***********************************************
1. Llamamos a la Biblioteca "Graphics,Legend"
***********************************************)

Needs["Graphics`Legend`"]

El Código siguiente define la función f, el punto al que se le calcula el límite, se resaltan los valores del límite y los puntos sobre los ejes y el gráfico que intervienen en el “acercamiento” de los valores de x hacia el punto x = 1. Además se consideran las rectas y el gráfico con colores diferentes. Este modelo puede ser fácilmente modificado para otras situaciones.

(**********************************************
2. Limpiamos la Variable de la Función
***********************************************)
Clear[f];
(**********************************************
3. Definimos la Función
***********************************************)
f[x_ ] := (x2-1)/(x-1);
(**********************************************
4. Graficamos la Idea Intuitiva de Límite
***********************************************)
Do [ Plot[{f[x],2,e+2,-e+2,2.5,1.5},{x,0,2}],
Ticks -> {{0.5,1,1.5},Automatic},
PlotRange->{0,4}
PlotStyle->{RGBColor[1,0,0],
RGBColor[0,0,1],
Dashing[{0.03}],
Dashing[{0.03}],
RGBColor[0.2,0.2,0.2],
RGBColor[0.3,0.3,0.3]},
Epilog->{
(* Se marcan los puntos representativos *)
PointSize[0.015],Hue[0.6],Point[{1,2}],
PointSize[0.013],Hue[1],Point[{e+1,e+2}],
PointSize[0.013],Hue[1],Point[{-e+1,-e+2}], PointSize[0.013],Hue[1],Point[{e+1,0}],
PointSize[0.013],Hue[1],Point[{-e+1,0}], 
PointSize[0.013],Hue[1],Point[{0,e+2}], 
PointSize[0.013],Hue[1],Point[{0,-e+2}], 
PointSize[0.015],Hue[0.6],Point[{0,2}], PointSize[0.015],RGBColor[0.3,0.3,0.3],Point[{0,2.5}], PointSize[0.015],RGBColor[0.3,0.3,0.3],Point[{0,1.5}], PointSize[0.015],RGBColor[0.3,0.3,0.3],Point[{0.5,0}], PointSize[0.015],RGBColor[0.3,0.3,0.3],Point[{1.5,0}], PointSize[0.015],Hue[0.6],Point[{1,0}],},
(**********************************************
5. Generamos una etiqueta para el gráfico
***********************************************)
PlotLegend->{Función, Límite, 2+e,2-e, y=2.5,y=1.5},
LegendPosition->{2,-0.5}],{e,-0.5,0.5,0.1}]

La salida es una secuencia de imágenes similares a la siguiente con las cuales se construye la animación. Estas imágenes se pueden guardar como archivos BMP o metafile. De esta forma, mediante programas como Adobe Photoshop se puede mejorar la imagen y la animación eventualmente se puede montar en otras plataformas como Flash o Director. Así, también es posible crear vídeos con extensión AVI a partir de estos últimos. 

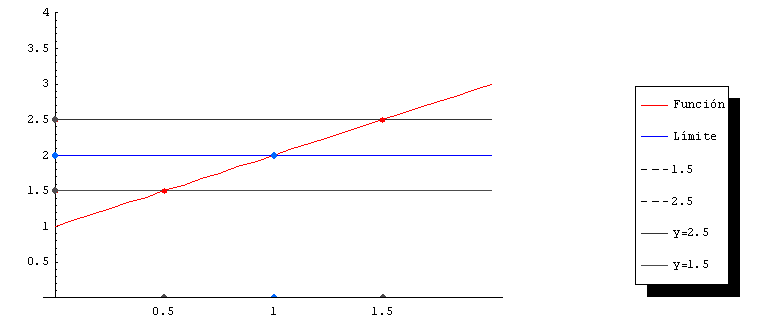
El siguiente código genera una animación para visualizar el concepto de Derivada como pendiente de la recta tangente a la curva en un punto.
(******************************************
1. Definimos la función
******************************************)
f[x_ ] := -(x-3)2+4
Do[Plot[{
(*1. Se grafica la función f *) 
f[x],
(* 2 Se grafica la recta tangente *) 
f ´ [2] x + (3-f ´ [2] * 2),
(* 3. Se grafica la recta secante inicial *)
(f[3.75]- f[2]) / (3.75 – 2) x+ (3- (f[3.75]-f[2]) / (3.75 -2) * 2),
(* 4. Se grafican las rectas secantes paramétricas*)
(f[2+h]- f[2]) / h *x+ (3- (f[2+h]-f[2]) / h * 2)},
{x,-1,7},
PlotRange -> {-3,6},
AspectRatio -> 0.5,
Ticks ->{{ 2,2+h},Automatic}, 
PlotStyle-> {RGBColor[1,0,0],
RGBColor[0,0,1],
RGBColor[0.1,0.1,0.1],
RGBColor[0.2,0.3,0.3]},

(*Se plotean los puntos clave*)

Epilog ->{
PointSize[0.016],Hue[0.6], Point[{2,f[2]}], 
PointSize[0.016],Hue[1], Point[{3.75,f[3.75]}], 
PointSize[0.016],Hue[1], Point[{2+h,f[2+h]}],}], (*cerramos el Plot*) 
{h,1.75,0.01,-0.1}] (*cerramos el Do*)

La salida muestra el movimiento de la recta secante en el siguiente gráfico:

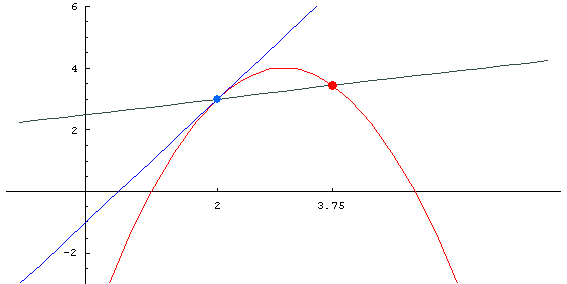
La animación muestra como el punto rojo se desplaza a lo largo de la curva y tiende al punto azul conforme el punto del eje x tiende al punto x=2.
De estos ejemplos podemos deducir que el diseñador de instrumentos educativos audiovisuales, debe tener conocimiento de la plataforma . Ya sea MATHEMATICA 5.0 o cualquier otra aplicación, la construcción de imágenes y animaciones demanda una gran cantidad de tiempo y preparación. 

Aspectos Metodológicos de las presentaciones para Cálculo Diferencial e Integral

La preparación de material de práctica pone de relieve otro aspecto que debe ser considerado. Dado que en todo curso de matemática existe un cierto porcentaje de estudiantes que repite la materia, el material presentado debe de estarse renovando continuamente. Esto implica que implementar laboratorios en los cursos de matemática demanda una cantidad considerable de tiempo y aunque algunos de los materiales elaborados como las animaciones pueden ser reutilizados otros como las prácticas de laboratorio deben ser modificadas después de cierto tiempo. 
Cuando se trabaja una plataforma multimedial en la producción de instrumentos educativos, con frecuencia notamos que la interface visual no es la optima para nuestros propósitos. En este caso, es conveniente salvar las imágenes y procesarlas en un editor de imagen como Adobe Photoshop, Ilustrador, etc y posteriormente montar la animación. El principio que se sigue es que la presentación de un instrumento multimedial debe de respetar la calidad gráfica
Esta situación, hace que el trabajo de producción de materiales no debe recaer en una sola persona sino que se deben de conformar grupos de trabajo en las diferentes cátedras para ir conformando un banco de materiales que permita con el paso del tiempo tener suficiente material de referencia.
La ventaja que presenta la producción de este tipo de instrumentos es que una vez que se tiene el concepto de lo que se quiere graficar y se ha hecho al menos un prototipo, es más fácil modificar y perfeccionar el instrumento a partir de este primero. Por ejemplo, las animaciones mostradas en el apartado anterior se pueden modificar para presentar otras gráficas de funciones pero con el los mismos componentes conceptuales. Así, se puede generar variedad visual del mismo tema. Otra ventaja es que la facilidad de guardar el material elaborado, hace que el banco de recursos se mantenga a través del tiempo y pueda servir de referencia para cursos de capacitación de otros profesores y de consulta para los alumnos.

Conclusiones 

La producción de materiales multimediales para cálculo diferencial e integral plantea serias dificultades de muy diversa índole. En primera instancia esta el aspecto presupuestario el cual limita la posibilidad de escoger una herramienta adecuada para el desarrollo de los instrumentos educativos. En segundo lugar esta la capacitación del cuerpo docente pues aunque se tenga las aplicaciones adecuadas se debe contar con los desarrolladores de aplicaciones. Estos a su vez deben de tener un perfil que les permita determinar los aspectos no solo de contenido sino también a nivel técnico de la aplicación y de manejo de la imagen audiovisual. Esto indica que el especialista en contenido, esto es, el profesor de matemática como tal debe complementar su formación con estos otros aspectos para poder desarrollar materiales multimediales en matemática.
Por otro lado, se mostró como la producción de aplicaciones educativas demanda gran cantidad de tiempo de trabajo en su implementación lo cual contrasta con el hecho de que deben de ser modificadas con el tiempo para no crear redundancia en aquellos estudiantes que deban repetir la materia. Esto a su vez plantea la necesidad de conformar equipos de trabajo que con el tiempo construyan una base de datos que permita facilitar el uso del recurso audiovisual.

Bibliografía.

[1] Bou, Guillén. El Guión Multimedia. Anaya Multimedia. 1997. Págs 28-30,66-68
[2] Quiros, Luis. Diseño. Teoría acción y sentido.Editorial Tecnológica de Costa Rica. 1998. Págs 48-54
[3] Wolfram, Stephen. The MATHEMATICA book . Fourth Edition
[4] Díaz Pedro. Apuntes del Curso Software Educativo en Matemática. Universidad de Costa Rica. 2004