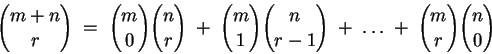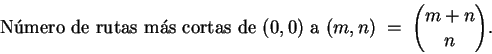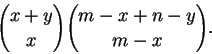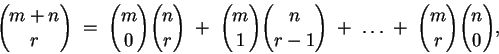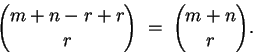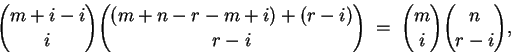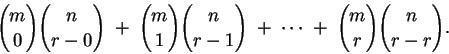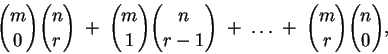Sobre una fórmula en Combinatoria.
José Rosales Ortega
Escuela de Matemática
Instituto Tecnológico de Costa Rica
La idea del siguiente arículo surgió al leer el libro [2].
Allí se exponen los rudimentos de la teoría de combinatoria que se
utilizan en la competencias de Olimpíadas Matemáticas en México.
Nos proponemos mostrar las siguiente fórmula combinatoria:
Si 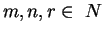 son tales que
son tales que 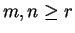 ,entonces ,entonces
Esta fórmula es muy famosa y se conoce como la fórmula de
Vandermonde. De hecho el lector puede consultar [1]
para obtener una demostración usando métodos totalmente distintos al
usado aquí. Los métodos que utiliza el autor para demostrar la fórmula
anterior se basan en la manipulación de identidades combinatorias y de
las llamadas funciones generadoras.
Para lograr nuestro objetivo nos valdremos de un método muy sencillo
pero no muy conocido: el método de contar el número de rutas más
cortas entre dos puntos del plano.
Definición 1 Un punto 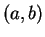
en el plano cartesiano se llama punto reticular si tanto 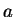
como 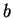
son números enteros.
Los puntos reticulares se obtienen de una manera muy fácil. En el
plano cartesiano considere 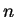 puntos en el semieje positivo de las
puntos en el semieje positivo de las 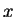 ,
y ,
y 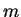 puntos en el semieje positivo de las
puntos en el semieje positivo de las 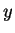 .
Si por cada uno de los .
Si por cada uno de los 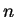 puntos trazamos una línea paralela al semieje de las
puntos trazamos una línea paralela al semieje de las 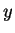 y otra paralela al eje de las
y otra paralela al eje de las 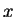 por cada uno de los
por cada uno de los 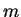 puntos, entonces obtenemos una cuadrícula con
puntos, entonces obtenemos una cuadrícula con 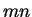 rectángulos.
rectángulos.

Recordemos que una sucesión de números
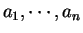 se llama sucesión binaria si cada
se llama sucesión binaria si cada 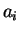 es 0 ó 1, para cada
es 0 ó 1, para cada 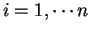 .
La longitud de una sucesión binaria se define como el número de términos
de la sucesión. Por ejemplo, en la sucesión binaria 1,1,0,0,1,0,1 la
longitud es 7. Queremos responder a la siguiente pregunta: cuántas
sucesiones binarias hay de longitud .
La longitud de una sucesión binaria se define como el número de términos
de la sucesión. Por ejemplo, en la sucesión binaria 1,1,0,0,1,0,1 la
longitud es 7. Queremos responder a la siguiente pregunta: cuántas
sucesiones binarias hay de longitud 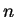 ?
Para fijar ideas veamos cuántas sucesiones binarias hay de longitud 7.
La respuesta es muy simple, existen ?
Para fijar ideas veamos cuántas sucesiones binarias hay de longitud 7.
La respuesta es muy simple, existen 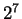 sucesiones binarias de longitud 7. Para ver esto nótese que para elegir
el primer elemento de nuestra sucesión tenemos dos posibilidade 0 ó 1,
para el segundo las mismas dos posibilidades y así sucesivamente, para
en resumen tener
sucesiones binarias de longitud 7. Para ver esto nótese que para elegir
el primer elemento de nuestra sucesión tenemos dos posibilidade 0 ó 1,
para el segundo las mismas dos posibilidades y así sucesivamente, para
en resumen tener 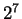 posibilidades. En general, el número de sucesiones binarias de longitud
posibilidades. En general, el número de sucesiones binarias de longitud
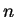 es dado por
es dado por 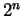 . .
Ahora nos proponemos responder una pregunta un poco más difícil: cuántas
sucesiones binarias de longitud 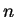 ,
que consten de ,
que consten de 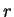 -ceros
y -ceros
y 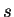 -unos,
existen, con -unos,
existen, con 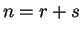 ?
Una vez más, para fijar ideas consideremos sucesiones binarias de
longitud 7 y que consten de cuatro ceros y tres unos, por ejemplo, la
sucesión 1,0,0,0,1,0,1. Nótese que para formar una tal sucesión
primero elegimos ?
Una vez más, para fijar ideas consideremos sucesiones binarias de
longitud 7 y que consten de cuatro ceros y tres unos, por ejemplo, la
sucesión 1,0,0,0,1,0,1. Nótese que para formar una tal sucesión
primero elegimos
Consideremos
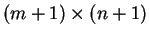 puntos reticulares como en la figura anterior.
puntos reticulares como en la figura anterior.
La pregunta que nos hacemos es cuántas rutas más cortas hay desde 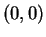 hasta
hasta 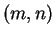 ?
Una tal ruta se muestra en la figura anterior. Recordemos que tales
rutas se pueden pensar como sucesiones binarias finitas. Cada una de
estas sucesiones binarias consta de ?
Una tal ruta se muestra en la figura anterior. Recordemos que tales
rutas se pueden pensar como sucesiones binarias finitas. Cada una de
estas sucesiones binarias consta de 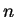 ceros y de
ceros y de 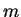 unos, si identificamos cada segmento vertical con un 0 y cada segmento
horizontal con un 1. Luego el problema de encontrar el número de rutas
más cortas entre
unos, si identificamos cada segmento vertical con un 0 y cada segmento
horizontal con un 1. Luego el problema de encontrar el número de rutas
más cortas entre 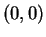 y
y 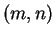 se traduce en encontrar el número de sucesiones binarias de longitud
se traduce en encontrar el número de sucesiones binarias de longitud 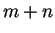 con
con 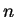 ceros y
ceros y 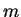 unos. Usando los mismos argumentos del inicio de este artículo
encontramos que
unos. Usando los mismos argumentos del inicio de este artículo
encontramos que
La siguiente observación será fundamental para la demostración de
la primera fórmula que nos propusimos deducir al inicio del artículo.
Para ello nos basaremos en la siguiente figura:
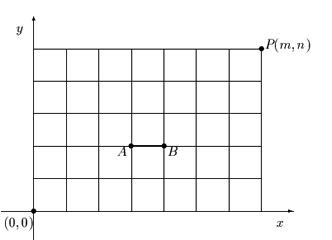
Supongamos que las coordenadas del punto 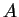 son
son 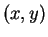 y las de
y las de 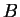 son
son  .
Ahora nos preguntamos por el número de rutas más cortas desde .
Ahora nos preguntamos por el número de rutas más cortas desde 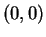 hasta
hasta 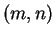 y que pasen por el punto
y que pasen por el punto 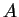 .
Para dar respuesta a esta pregunta procederemos de la siguiente manera.
Primero encotraremos el número de rutas más cortas desde .
Para dar respuesta a esta pregunta procederemos de la siguiente manera.
Primero encotraremos el número de rutas más cortas desde 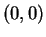 hasta
hasta 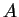 y luego el número de rutas más cortas desde
y luego el número de rutas más cortas desde 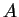 hasta
hasta 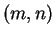 .
El resultado será entonces el producto de éstos dos. El primero de
estos números es dado por .
El resultado será entonces el producto de éstos dos. El primero de
estos números es dado por
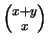 y el segundo está dado por
y el segundo está dado por
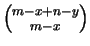 .
Por lo tanto, el número de rutas más cortas de .
Por lo tanto, el número de rutas más cortas de 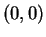 a
a 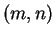 y que pasan por
y que pasan por 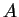 es igual a
es igual a
Demostremos ahora la siguiente fórmula:
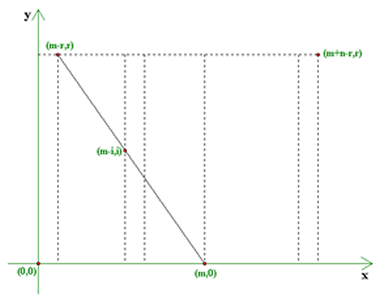
donde 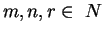 son tales que
son tales que 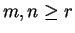 . .
Consideremos la siguiente figura:
Nótese que el número de rutas más cortas entre 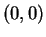 y
y 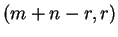 es dado por
es dado por
Lo anterior no es nada más y nada menos que el lado izquierdo de la
fórmula anterior. Para terminar vamos a calcular de nuevo el número de
rutas más cortas entre 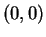 y
y 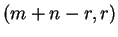 ,
pero en una forma diferente. ,
pero en una forma diferente.
Consideremos el segmento de línea uniendo los puntos
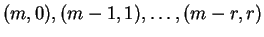 ,
tal y como se indica en la figura anterior. Notemos que cada ruta más
corta entre ,
tal y como se indica en la figura anterior. Notemos que cada ruta más
corta entre 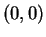 y
y 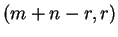 pasa sólo por uno de estos puntos. El número de rutas más cortas que
pasan por el punto
pasa sólo por uno de estos puntos. El número de rutas más cortas que
pasan por el punto 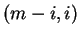 es dado por
es dado por
para cada 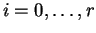 . .
Luego el número total de rutas entre 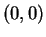 y
y 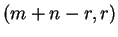 será la suma del número de rutas más cortas que pasan por el punto
será la suma del número de rutas más cortas que pasan por el punto 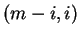 ,
para ,
para
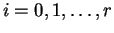 ,
y tal suma es ,
y tal suma es
En resumen, el número de rutas más cortas entre 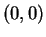 y
y 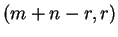 es dado por
es dado por
que es el lado derecho de la fórmula a demostrar.
- 1
- Daniel I. A. Cohen , Basic Techniques of Combinatorial Theory,John
Wiley & Sons, Canada 1978.
- 2
- María Luisa Pérez Seguí , Combinatoria, Cuadernos de
Olimpiadas Matemáticas, México, 2000.
This document was generated using
the LaTeX2HTML
translator Version 99.2beta6 (1.42)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University, Sydney.
|