Inicio
Jugando con fractales en el Geómetra Sketchpad
Luis Ernesto Carrera Retana
Profesor de la
Escuela de Matemática
Instituto Tecnológico de Costa
Rica
Introducción
El tema de los fractales es en verdad apasionante, y tal vez una forma interesante para introducir algo de matemática en los jóvenes estudiantes. En esta ocasión, este artículo tiene el fin de ser una introducción al trabajo de fractales en el Geómetra, utilizando básicamente el comando de iteración. También se mostrarán algunos trucos que nos pueden servir tanto para mejorar el resultado de nuestro trabajo, así como para mostrar una amplia gama de fractales diferentes, todos generados del mismo origen, pero con formas muy diferentes entre si, simplemente animando un parámetro.
Una pequeña introducción: El conjunto de Cantor
La idea básica de un fractal, es que éste exhibe recursividad o autosimilitud: cuando observamos cualquier parte de él, vemos el patrón original de la figura completa. Nos brincaremos la definición formal del conjunto de Cantor, pero tiene como idea mostrar que después de quitar infinitas cantidades de una recta numérica, los elementos que nos quedan siguen siendo infinitos no numerables.
Gráficamente el conjunto de Cantor es bastante interesante, y nos muestra la naturaleza básica de los fractales. Comenzamos con un segmento de recta. Para poder ir observando el progreso de la iteración vamos a ir colocando la siguiente iteración en un "renglón aparte".
El procedimiento en Sketchpad consiste en:
- Dibujar un segmento de recta original, que supongamos es horizontal. (Para que la recta quede completamente horizontal, deje apretada la tecla Mayúscula mientras la dibuja).
- Luego, trasladar sus puntos hacia abajo. Esto es para empezar nuestro "renglón aparte". Para trasladarlos, los seleccionamos únicamente a ellos, y seleccionamos Transformar | Trasladar..., y ponemos en la casilla de distancia fija el valor de 1 cm, y en la de ángulo fijo -90º y hacemos click en "Trasladar".
- Ahora hacemos la parte "importante". La idea del conjunto de Cantor es borrar la tercera parte de la recta que corresponde a la parte central. Así, hacemos doble click en el punto izquierdo que acabamos de trasladar, y vemos que se produce una animación de círculos concéntricos sobre él. Esto es lo mismo que seleccionar el punto y ejecutar el comando Transformar | Marcar centro. Luego, seleccionamos el punto derecho, y ejecutamos Transformar | Dilatar... dos veces, primero con 1/3 y luego con 2/3, y dibujamos los 2 segmentos de recta de los lados.
- Y nuestro siguiente paso es hacer la iteración para tener nuestro fractal. Seleccionamos nuestros puntos originales, es decir con los que dibujamos nuestra recta. Luego ejecutamos Transformar | Iterar..., y asociamos los dos puntos con nuestro nuevo segmento izquierdo. Luego en Estructura | Nuevo mapeo (Ctrl + A), y asociamos los puntos originales con nuestro segmento derecho. ¡Y listo!, ya tenemos el fractal del "polvo de Cantor" después de hacer click sobre Iterar. Recordemos que para aumentar o disminuir nuestro número de iteraciones, seleccionamos la iteración y utilizamos (+) y (-)
respectivamente.
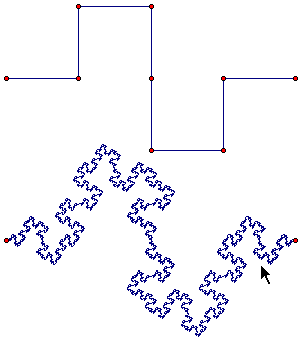
El fractal de la caja
Nuestro trabajo consiste en dibujar el siguiente fractal:
Para ello, sigamos los siguientes pasos:
- Dibujemos dos puntos que estén alineados de manera horizontal. Estos puntos van a ser nuestra "tapa".
- Dibujemos los otros dos puntos de la base que completarían el cuadrado. (Existen varias formas para ello; una simple consiste en rotar uno de los puntos, tomando el otro como eje, en 90º o -90º).
- Seleccionemos los puntos y dibujemos el interior del cuadrado (Construir | Interior del cuadrilátero, o con el comando (Ctrl + P)). Si no obtiene un cuadrado sino dos triángulos, debe borrar lo que hizo, y tomar los puntos en orden: Empezar en la izquierda arriba, ir hacia la derecha, luego hacia abajo y finalmente a la izquierda. Intente nuevamente construir su cuadrilátero (Con el botón derecho del ratón nos aparece la posibilidad para cambiar el color, por si acaso no les gusta el amarillo que trae ya como predeterminado).
- Ahora debe hacer una "malla" de puntos, utilizando el comando Transformar | Dilatar..., siempre utilizando una razón de 1/3 o 2/3, de manera que se haga una cuadrícula como la siguiente:
- Ahora hacemos la iteración. Como los puntos originales están "arriba", y los construidos están "abajo", así, a la hora de iterar, debo seleccionar solamente los puntos superiores, y construyo cinco mapeos, cada uno que corresponda a la parte superior del cuadrado que quiero hacer.
- Aquí nos enfrentamos a un par de cosas. Al finalizar la iteración anterior no se ve nada, solamente el cuadrado original, pues todos los cuadrados están rellenos del mismo color. En algunos casos (y este es uno de ellos), no es bueno tener todas las iteraciones, sino solamente la iteración final. Para ello, primero ocultamos nuestro cuadrilátero original, y luego, haciendo click derecho sobre la iteración, en Propiedades | Iteración seleccionamos Únicamente iteración final.
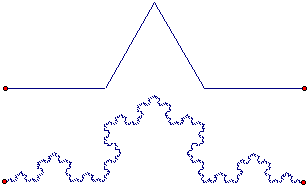
Ya podrían intentar hacer las siguientes iteraciones, que corresponden al generador y al resultado de la curva de Koch en dos formas distintas:
En ambos casos se muestra únicamente la iteración final, y se ocultan los segmentos originales. El famoso copo de nieve de Koch, es el primero de estos casos, cuando se construye sobre un triángulo
equilátero.
El triángulo de Serpinsky, y algunas deformaciones
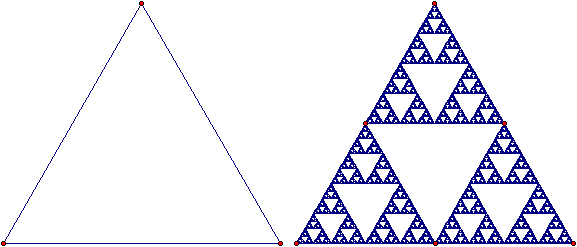
El triángulo de Serpinsky es tal vez uno de los fractales más conocidos:
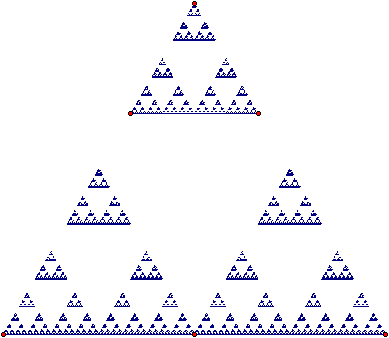
Este se contruye tomando los puntos medios de los lados, y haciendo 3 mapeos del triángulo original sobre cada una de las esquinas. Sin embargo, podríamos también tomar una tercera parte de los segmentos con respecto al punto superior, y nos quedaría algo así:
Una deformación interesante que observé una vez en un taller fue la siguiente:
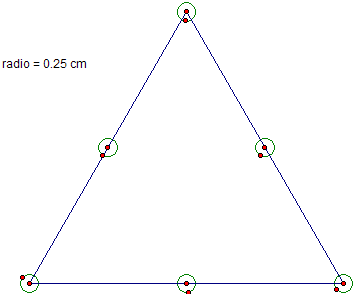
- Se construye un triángulo equilátero, se construyen sus puntos medios, y con una medida dada como parámetro (nótese que el parámetro debe tener unidades en centímetros) se construyen círculos sobre sus puntos medios y sobre los vértices del triángulo (se seleccionan los puntos medios y el parámetro, y se selecciona el comando Construir | Círculos por centros + radio.
- Seleccionar los círculos, y construir puntos sobre ellos. Luego ocultar los círculos (pero no los puntos que construimos sobre ellos). Una forma rápida de hacerlo es seleccionar el círculo en nuestra barra de herramientas, y luego (Ctrl-A) para seleccionar "todos" los círculos, y (Ctrl-H) para ocultarlos.
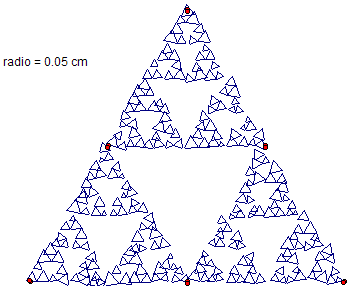
- Finalmente hacer la iteración, pero no sobre los puntos del triángulo, sino sobre los puntos en el círculo. Sin embargo, hay que hacer un par de modificaciones antes de hacer click sobre el botón iterar. Primero, en Estructura | A nuevas posiciones aleatorias, y luego, en Mostrar | Únicamente iteración final.
- Ocultamos el triángulo original, y disminuimos el parámetro a 0.05cm. Podemos observar una "degradación" interesante, si en las propiedades del parámetro (click derecho sobre el parámetro), en parámetro, ponemos el ajuste del teclado en 0.01 unidades. Luego, con el parámetro seleccionado y las teclas (+/-) lo modificamos.
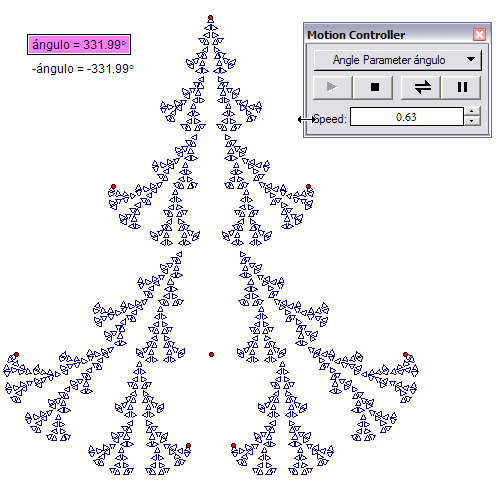
También se puede mostrar una animación interesante, rotando los triángulos inferiores en ángulos opuestos. Para ello siga los siguientes pasos:
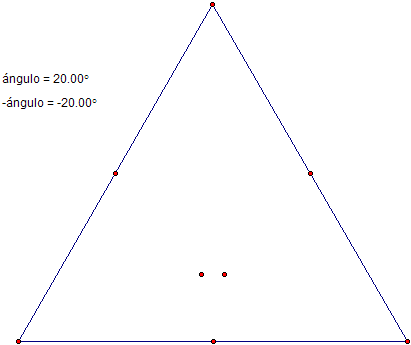
- Después de construir el triángulo equilátero, construya un parámetro con unidades en grados, y construya una medida que sea -ángulo.
- Construya los puntos medios, y rote el punto de la base dos veces, una vez con la medida positiva y el vértice inferior izquierdo, y la otra con la medida negativa y el vértice inferior derecho:
- Construya la iteración, utilizando los puntos rotados, y mostrando solamente la iteración final. Aumente el número de iteraciones, y anime el primer parámetro.
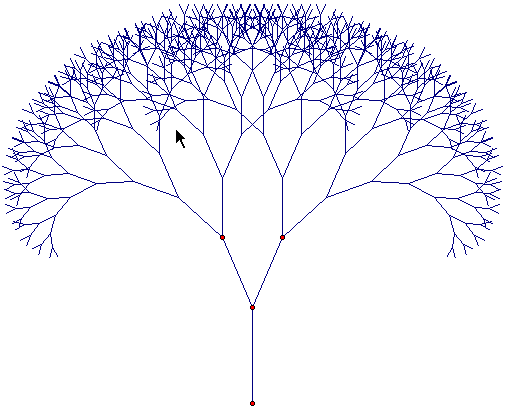
Construyendo árboles
- Comenzamos con un segmento de recta vertical y 3 parámetros, donde dos de ellos son ángulos, uno un parámetro y el segundo un cálculo = (-angulo) (recordemos colocar sus unidades en la casilla correspondiente), y el otro es una escala negativa, la cual no lleva unidades (el hecho de que sea negativa, se debe a que vamos a utilizar Dilatar, pero necesitamos que la dilatación no sea sobre el segmento de recta, sino al lado contrario):
- Hacemos doble click sobre el punto superior (Seleccionar punto y Transformar | Marcar centro), y seleccionamos el parámetro de escala y Transformar | Marcar factor de escala.
- Hacemos click sobre el punto inferior, y Transformar | Dilatar, y luego click sobre Dilatar.
- Tomamos el punto recién construido, y lo rotamos alrededor del punto superior (no hace falta marcarlo como centro, pues ya estaba definido así para la construcción anterior) con las dos medidas de ángulos. Recordemos en cada caso seleccionar el ángulo y (-ángulo) en Transformar | Marcar ángulo.
- Ocultamos el punto construido por la dilatación, e iteramos: tomamos los puntos del segmento original, y hacemos dos mapeos correspondientes a cada uno de los lados. Y listo.
Modificar los parámetros nos presentan una nueva variedad de fractales distintos, todos interesantes.
Esperamos que las actividades aquí mostradas les animen a investigar y a jugar más con el geómetra Sketchpad, con el cual se pueden realizar muchas actividades interesantes.
Aquí, como siempre, el archivo .gsp donde pueden encontrar las actividades realizadas acá en este
artículo.
|