Computación Distribuida

La Computación Distribuida es la rama de las Ciencias Computacionales que estudia la ejecución de un algoritmo por medio de varios sitios, dispersos geográficamente, que comparten recursos.

El modelo que utilizaremos en este artículo ([7]) supondrá varios elementos:

Sitio: localidad donde se está ejecutando un programa.
Evento: mínima unidad en la ejecución de un programa.
Mensaje: envío de información de un sitio a otro.

Figura 1: Historia distribuida

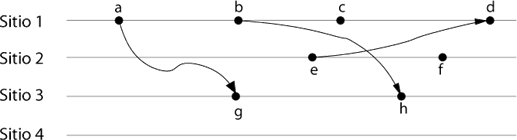
En la figura 1 se muestra la representación gráfica de una historia distribuida. En la misma se puede apreciar un sistema distribuido con 4 sitios, donde cada línea representa la ejecución en el tiempo de un programa compuestos por varios (inclusive ningún) eventos. Los círculos negros son los eventos que ocurren en cada uno de los sitios. Así pues, el evento a es el primero del sitio 1. Finalmente, las flechas indican la propagación de un mensaje de un evento a otro. Entonces, existe un mensaje que parte del evento a y llega al evento g.

La Historia Local del sitio es una secuencia de eventos $\mathcal{H}_i = e_1e_2...$ que son ejecutados en ese sitio. Hay un orden total en los eventos locales en cada sitio. La Historia Global $\mathcal{H}$ del sistema distribuido (o simplemente, historia distribuida) es el conjunto de todos los eventos que ocurren en todos los sitios del sistema.

Existen solo 3 clases de eventos: ENVIO, RECEPCION e INTERNO. Dado esto, en la figura 1, el evento a es un ENVIO, mientras que g es un RECEPCION y aquellos que no sean ninguno de los anteriores se dicen INTERNO, como el evento c.

Una de las relaciones más importantes entre los eventos es la causalidad. Por causalidad se entiende que un evento a previo a un evento g podría ser la causa del último. Entonces, la causalidad que se trata de determinar es potencial. En la figura 1, el evento a es una causa potencial del evento g, porque precisamente a es el envío de un mensaje que es recibido posteriormente por g. Además, a es una causa potencial de b, dado que ocurre antes en el sitio 1. El tema de causalidad supone un ordenamiento de los eventos en una historia distribuida.

Para poder detectar este ordenamiento, se podrían utilizar relojes físicos y comparar el tiempo en que fue ejecutado cada evento para así determinar cuál es el orden de causalidad entre ellos. Empero, esta estrategia adolece de muchas complicaciones, debido a la sincronización de tales relojes.

Entonces, en el seminal artículo ([6]), Leslie Lamport describe los relojes lógicos como un mapeo entre eventos en una historia distribuida y el conjunto de los números enteros, de manera que se captura el orden causal.

Lamport ([6]) definió la relación de causalidad " $\rightarrow$ '' (happens before), como la relación más pequeña, tal que:

si $e_{ij}$ y $e_{ik}$ $\in$ $\mathcal{H}_i$ y entonces $e_{ij}\rightarrow e_{ik}$ .
si $e_{im}$ es el evento ENVIO( $\mathcal{M}$ ), $e_{jn}$ es el evento RECEPCION( $\mathcal{M}$ ) y $\mathcal{M}$ es el mismo mensaje en ambos casos, con , , y arbitrarios, se tiene que $e_{im} \rightarrow e_{jn}$ .
si , y $\in \mathcal{H}$ , si $a \rightarrow b$ y $b \rightarrow c$ entonces $a \rightarrow c$ .

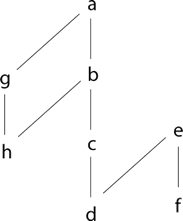
Si entre dos eventos y , no sucede ni $a \rightarrow b$ , ni $b \rightarrow a$ , entonces se dice que y son concurrentes. Denotaremos esta situación como || . Como la relación de causalidad $\rightarrow$ es irreflexiva y transitiva, entonces define un orden parcial estricto $\langle H, \rightarrow \rangle$ sobre los eventos del sistema. Como orden parcial, tiene su correspondiente diagrama de Hasse ([3]).

Figura 2: Diagrama de Hasse

La figura 2 muestra el diagrama de Hasse correspondiente a la figura 1. La relación utilizada corresponde a " $\rightarrow$ '' (happens before), definida por Lamport([6]).

En la figura 2 se aprecian las relaciones de causalidad que aparecen entre los eventos de la historia distribuida. Para ejemplificar, el evento a es causalmente antes que h, lo cual es cierto, dado que a es el ENVIO de un mensaje que luego recibe g y además g ocurre localmente antes que h. Sin embargo, no se puede determinar la relación de causalidad que existe entre b y f, lo que los hace eventos concurrentes.

Revista digital Matemática, Educación e Internet.
Derechos Reservados