Un Problema de Conjuntos en Computación		Esteban Meneses,  Francisco J. Torres-Rojas.

Inicio  1  2  3  4  5  6	Versión PDF

 

Relojes Vectoriales

 

Los relojes vectoriales son un tipo de reloj lógico propuesto independientemente por Colin Fidge ([4]) y Friedemann Mattern ([8]). Interesantes recorridos sobre temas y aplicaciones de los mismos se puede encontrar en [1,10,11,12].

Esta técnica consiste en un mapeo entre eventos en una historia distribuida y vectores de enteros. Cada sitio $i$ mantiene un vector $V_i$ con $N$ entradas, donde $N$ es la cantidad de sitios en el sistema distribuido. Este vector ¹ se inicializa en ceros. La entrada $V_i[i]$ del sitio $i$ mantiene el reloj local, mientras que la entrada $V_i[j]$ mantiene el conocimiento actual que el sitio $i$ tiene de la actividad en el sitio $j$. Estos vectores se incrementan en el reloj local cada vez que ocurren eventos en el sitio. También, todo mensaje debe incluir el reloj vectorial que tenía el sitio emisor cuando el mensaje fue enviado, y al recibir mensajes, se debe actualizar el vector local, tomando en cuenta la etiqueta de tiempo incluida en cada mensaje.

El sitio $i$ actualiza su vector $V_i$ de acuerdo con las siguientes reglas:

V0:

$1 \leq j \leq N$: $V_i[j] = 0$

V1:

Cada vez que ocurre un evento local: $V_i[i] = V_i[i] + \Delta$, donde $\Delta$ es un valor entero positivo.

V2:

Al recibir un mensaje con etiqueta de tiempo $T$: $1 \leq j \leq N$: $V_i[j] = max(V_i[j], T[j]),\;$ $\;V_i[i] = V_i[i] + \Delta$.

Dado un evento $a \in \mathcal{H}$ se dice que la etiqueta de tiempo o el reloj vectorial asociado a $a$ es el reloj vectorial que tenía el sitio particular cuando $a$ fue ejecutado. Se denotará a este vector como $V(a)$.

Dados dos relojes vectoriales $v$ y $w$, se definen las siguientes comparaciones:

• $v = w \, \Longleftrightarrow \, 1 \leq j \leq N$: $v[j] = w[j]$
• $v \leq w \, \Longleftrightarrow \, 1 \leq j \leq N$: $v[j] \leq w[j]$
• $v < w \, \Longleftrightarrow \, v \leq w$ y $\exists j$ tal que $v[j] < w[j]$
• $v$ || $w \, \Longleftrightarrow \, \exists k$ tal que $v[k] < w[k]$ y $\exists j$ tal que $v[j] > w[j]$

Mattern demostró en [8] que existe un isomorfismo entre los tiempos que se obtienen de un reloj vectorial cuando los eventos son ejecutados y la relación de causalidad entre los eventos de $\mathcal{H}$. Eso significa que $\forall a,b \in \mathcal{H}$:

• $a = b \, \Longleftrightarrow \, V(a) = V(b)$
• $a \rightarrow b \, \Longleftrightarrow \, V(a) < V(b)$
• $a$ || $b \, \Longleftrightarrow \, V(a)$ || $V(b)$

Esta característica es conocida como la condición fuerte de reloj (strong clock condition, [8,10,12]).

 

Figura 3: Etiquetas vectoriales de la figura

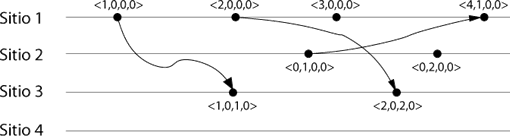
En la figura 3 se pueden observar las etiquetas vectoriales para los eventos de la historia distribuida de la figura 1. Estas etiquetas se obtuvieron al aplicar las reglas de generación de los relojes vectoriales (V0,V1 y V2), utilizando $\Delta=1$.

Por otra parte, si se recolectan las etiquetas vectoriales de esta historia distribuida se obtiene un conjunto de vectores: $\{<1,0,0,0>,<2,0,0,0>,<3,0,0,0>,<4,1,0,0>,<0,1,0,0>,<0,2,0,0>,<1,0,1,0>,<2,0,2,0>\}$. A este conjunto se le denominará conjunto posible, dado que existe una historia distribuida que puede generar todas las etiquetas de ese conjunto (aquella de la figura 1). También son conjuntos posibles: $\{<1,0,0,0>,<0,1,0,0>,<1,0,1,0>\}$ y $\{<1,0,0,0>\}$.

Contrariamente, un conjunto imposible es aquel conjunto de etiquetas vectoriales para el cual es imposible construir una historia distribuida que contenga todos esos vectores. Hay muchos de ellos y obtenerlos es sencillo ([9,11]).

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados