|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1 2 3

 

 

 

 

Método de los coeficientes indeterminados

Vamos a limitar nuestro estudio al enunciado y manejo del método, sin entrar en los detalles teóricos del mismo. Recuerde que una serie de potencias representa a una función $f$ en un intervalo de convergencia $I$ y que podemos derivarla sucesivamente, para obtener series para $f^{\prime}$, $f^{\prime \prime}$, $f^{\prime \prime \prime}$, etc. Por ejemplo,

$$\begin{eqnarray*} f(x) & = & a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots = \sum_{i... ...x^3 + \ldots = \sum_{n=0}^{\infty} n \left( n-1 \right) x^{n-2} \end{eqnarray*}$$

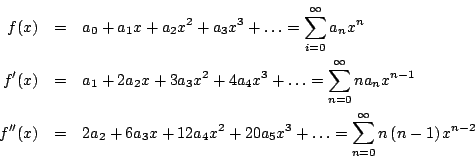Los siguientes ejemplos muestran como aplicar el método de las series de potencias a la solución de ecuaciones diferenciales. Iniciamos con un ejemplo muy simple, pero que nos hará entender la mecánica del método.

Ejemplo
Usando series de potencias halle la solución de la ecuación $y^{\prime} - 2y = 0$.

Solución

Supongamos que la solución se puede expresar como

$$y = \sum_{n=0}^{\infty} a_n x^n$$

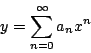
Entonces, $y^{\prime}$ esta dada por

$$y^{\prime} = \sum_{n=0}^{\infty} n a_n x^{n-1}$$

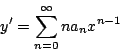
Sustituyendo en la ecuación diferencial, obtenemos que

$$\begin{eqnarray*} y^{\prime} - 2y & = & 0 \\ \sum_{n=0}^{\infty} n a_n x^{n-1... ...^{\infty} n a_n x^{n-1} & = & 2 \sum_{n=0}^{\infty} a_n x^n \\ \end{eqnarray*}$$

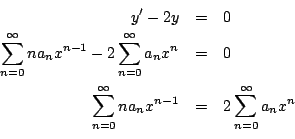
Ahora debemos ajustar los índices de las sumas de forma que aparezca $x^n$ en cada serie.

$$\sum_{n=-1}^{\infty} \left(n + 1 \right) a_{n+1} x^n = 2 \sum_{n=0}^{\infty} a_n x^n$$

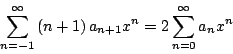
Igualando los coeficientes correspondientes

$$\left(n + 1 \right) a_{n+1} = 2 a_n \Rightarrow a_{n+1} = \frac{2a_n}{n+1}$$

para $n \geq 0$.

Esta fórmula genera los siguientes coeficientes

$$\begin{eqnarray*} a_1 & = & 2a_0 \\ a_2 & = & \frac{2a_1}{2}=\frac{2^2 a_0}{2... ...{2^4 a_0}{4!} \\ \vdots \\ a_n & = & \frac{2^n a_0}{n!} \\ \end{eqnarray*}$$

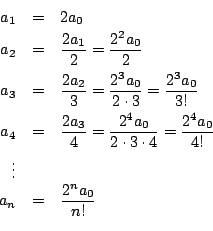De donde obtenemos que la solución esta dada por

$$y = \sum_{n=0}^{\infty} \frac{2^n a_0}{n!} x^n = a_0 \sum_{n=0}^{\infty} \frac{\left(2 x \right)^n}{n!} = a_0 e^{2x}$$

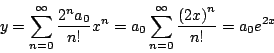
Aquí hemos usado la expansión en series de potencias para la función exponencial

$$e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}$$

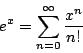
Observación: esta ecuación diferencial puede ser resuelta de manera más simple por medio de separación de variables.

$$y^{\prime} - 2 y = 0 \Rightarrow \frac{dy}{y} = 2 dx \Rightarrow Ln(y) = 2x + c \Rightarrow y = c e^{2x},$$

pero como digimos, la idea es ilustrar el método.

El siguiente ejemplo no puede ser resuelto por las técnicas estudiadas hasta el momento, a pesar de ser muy simple en apariencia.

Ejemplo
Usando series de potencias resuelva la ecuación diferencial $y^{\prime \prime} + x y^{\prime} + y = 0$

Solución

Suponga que

$$y = \sum_{n=0}^{\infty} a_n x^n$$

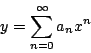
es una solución de la ecuación diferencial. Entonces

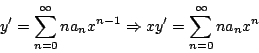
$$y^{\prime} = \sum_{n=0}^{\infty} n a_n x^{n-1} \Rightarrow xy^{\prime} = \sum_{n=0}^{\infty} n a_n x^n$$

y

$$y^{\prime \prime} = \sum_{n=0}^{\infty} n \left(n - 1 \right) a_n x^{n-2}$$

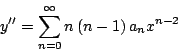
Sustituyendo en la ecuación diferencial

$$\begin{eqnarray*} \sum_{n=0}^{\infty} n \left( n-1 \right) a_n x^{n-2} + \sum_{... ...n-2} & = & -\sum_{n=0}^{\infty} \left(n + 1 \right) a_n x^n \\ \end{eqnarray*}$$

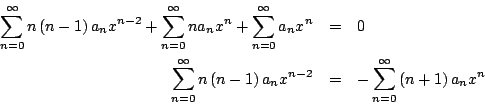Ajustando los índices

$$\sum_{n=-2}^{\infty} \left(n + 2 \right) \left(n + 1 \right... ...{n+2} x^n = - \sum_{n=0}^{\infty} \left(n + 1 \right) a_n x^n$$

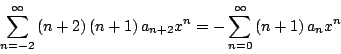
Igualando los coeficientes

$$a_{n+2} = - \frac{n + 1}{\left(n+2 \right) \left(n + 1 \right)} a_n = - \frac{a_n}{n+2}$$

para $n \geq 0$.

De esta forma los coeficientes de la serie solución están dados por:

• Coeficientes pares:
  $$\begin{eqnarray*} a_2 & = & - \frac{a_0}{2} \\ a_4 & = & - \frac{a_2}{4}= \fr... ...a_0}{2 \cdot 4 \cdot 6 \ldots (2n)} = \frac{(-1)^n a_0}{2^n n!} \end{eqnarray*}$$
  
  

• Coeficientes impares:
  $$\begin{eqnarray*} a_3 & = & - \frac{a_1}{3} \\ a_5 & = & - \frac{a_3}{5}= \fr... ...{2n+1} & = & \frac{(-1)^n a_1}{3 \cdot 5 \cdot 7 \ldots (2n+1)} \end{eqnarray*}$$
  
  

De esta forma la serie solución se puede representar como la suma de dos series, una para las potencias pares con coeficientes en términos de $a_0$ y otra para las potencias impares con coeficientes en términos de $a_1$.

$$y = a_0 \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{2^n n!} + ... ...infty} \frac{(-)^n x^{2n+1}}{3 \cdot 5 \cdot 7 \ldots (2n+1)}$$

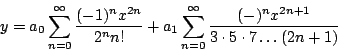
Observación: la solución tiene dos constantes arbitrarias $a_0$ y $a_1$ tal como era de esperar para una ecuación diferencial de segundo orden.

El siguiente ejemplo ilustra el procedimiento cuando la ecuación diferencial tiene condiciones iniciales.

Ejemplo

Use el teorema de Taylor^1.1 para hallar la solución en serie de potencias del problema de valor inicial

$$\left\{ \begin{array}{rcl} y^{\prime} & = & y^2 -x \\ y(0) & = & 1 \end{array} \right.$$

A continuación, use los primeros seis términos de la solución para aproximar los valores de $y$ en el intervalo $[0,1]$ con un paso de avance de $0.1$.

Solución

La solución $y$ del problema de valor inicial puede expresarse por medio del teorema de Taylor como

$$y = y(0) + \frac{y^{\prime}(0)}{1!} x + \frac{y^{\prime \prime}(0)}{2!} x^2 + \frac{y^{\prime \prime}(0)}{3!} x^3 + \ldots$$

con $c=0$. Como $y(0)=1$ y $y^{\prime} = y^2 - x$, tenemos que

$$\begin{eqnarray*} y^{\prime} = y^2 -x & \Rightarrow & y^{\prime}(0) = 1 \\ y^... ...me} \right)^2 & \Rightarrow & y^{(5)}(0) = 28 + 32 + 6 = 66 \\ \end{eqnarray*}$$

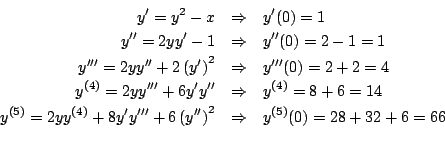De donde obtenemos que

$$y = 1 + x + \frac{1}{2} x^2 + \frac{4}{3!} x^3 + \frac{14}{4!} x^4 + \frac{66}{5!} x^5 + \ldots$$

Usando los seis primeros términos de esta serie, calculamos los valores de $y$ que se muestran en la siguiente tabla, además en la figura 1.1 se muestra la gráfica de este polinomio.

 

 

x	y	x	y
0	1	0.6	2.0424
0.1	1.1057	0.7	2.4062
0.2	1.2264	0.8	2.8805
0.3	1.3691	0.9	34985
0.4	1.5432	1	4.3
0.5	1.7620	1.1	528999

Observación: para una serie de Taylor entre más lejos estemos del centro de convergencia (en este caso $c=0$), menor es la precisión de nuestra estimación. Es importante tener claro que si las condiciones iniciales están dadas en $x=a$, debemos usar el desarrollo en series de potencias para la solución $y$ alrededor de $c=a$.

 

Figura 1.1: Gráfica de $y(x)$

Ejemplo

Encuentre una series de potencias para la solución general de la ecuación diferencial

$$y^{\prime \prime} + Sen(x) y^{\prime} + e^x y = 0$$

Solución

Como todos los coeficientes admiten desarrollo alrededor de $x=0$, podemos suponer que la solución $y$ es de la forma

$$y = a_0 + a_1x + a_2x^2 + a_3x^3 + \ldots + a_n x^n + \ldots = \sum_{n=0}^{\infty} a_n x^n$$

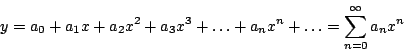
Además, recuerde que

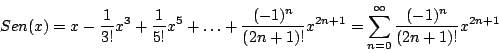
$$Sen(x) = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 + \ldots +... ...^{2n+1} = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1}$$

y

$$e^x = 1 +x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \ldots + \frac{1}{n!} x^n + \ldots = \sum_{n=0}^{\infty} \frac{1}{n!}x^n$$

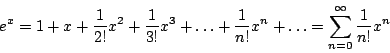
para toda $x \in \mbox{$I \hspace{-1.3mm} R$}$.

Sustituyendo en la ecuación diferencial obtenemos que

$$\begin{eqnarray*} \sum_{n=0}^{\infty} n\left( n-1 \right)a_n x^{n-2} + \left( \... ...}x^n \right) \left( \sum_{n=0}^{\infty} a_n x^n \right) & = & 0 \end{eqnarray*}$$

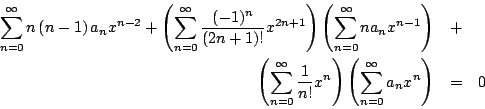Multiplicando las series y simplificando tenemos que

$$\begin{eqnarray*} \left(2a_2 + a_0 \right) + \left(6a_3 + 2a_1 + a_0 \right)x +... ..._2 + \frac{a_1}{2} + \frac{a_0}{6} \right) x^3 + \ldots & = & 0 \end{eqnarray*}$$

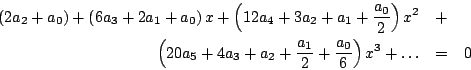Igualando cada uno de los coeficientes a cero

$$\begin{eqnarray*} a_2 & = & - \frac{a_0}{2} \\ a_3 & = & - \frac{2a_1 + a_0}{... ...ac{a_1}{60} - \frac{a_0}{120} = \frac{a_0}{20} + \frac{a_1}{20} \end{eqnarray*}$$

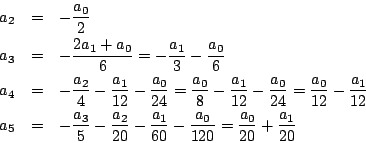Sustituyendo estos valores en la serie tenemos que

$$y = a_0 \left(1 - \frac{1}{2} x^2 - \frac{1}{6} x^3 + \frac... ...3} x^3 - \frac{1}{12} x^4 + \frac{1}{20} x^5 + \ldots \right)$$

para $x \in \mbox{$I \hspace{-1.3mm} R$}$.

Observación: algunas veces cuando necesitamos multiplicar dos series es útil la siguiente fórmula

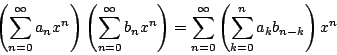
$$\left( \sum_{n=0}^{\infty} a_n x^n \right) \left( \sum_{n=0... ...m_{n=0}^{\infty} \left( \sum_{k=0}^{n} a_k b_{n-k}\right) x^n$$

 

 

Inicio Revista digital Matemática, Educación e Internet.