|
|
| 1 2 3 4 5 |
Funciones Logarítmicas:
Como hemos visto
las funciones exponenciales son funciones biyectivas, por lo tanto tienen
inversa 
. La inversa de una función exponencial de base a se
llama función logarítmica de base a , se representa por
, y se lee “logaritmo de x en base a”.
Definición:
, a>0, 
.
Mathematica define esta función como una función elemental usando: Log[b,z] para indicar el logaritmo en base b del número z.
Derive la define en forma muy similar, utilizando mayúscula y paréntesis, LOG(b, z).
Graficamos en Mathematica la función logaritmo de x en base 2.
Plot[Log[2,x], {x, 1/8, 8}, AxesLabel -> {x,y}]
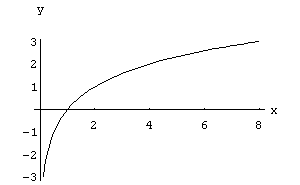
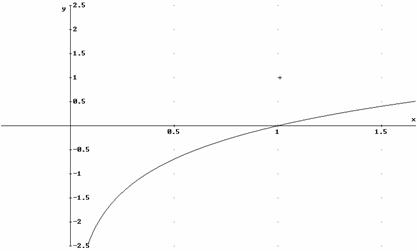
Con Derive:
La función logarítmica de base e se la denomina en Mathematica función logaritmo neperiano, y se representa: Log[x], comúnmente llamado logaritmo natural de x; la notación que aparece en muchos textos ln x, no es aceptada por Mathematica.
En Derive se define LN(x)
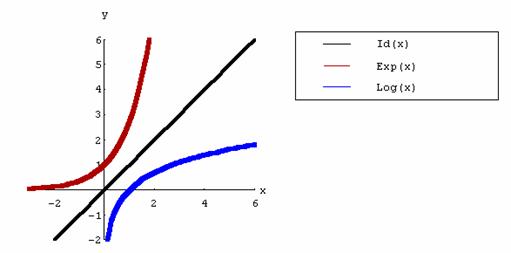
En Mathematica, graficamos las funciones identidad, exponencial y logarítmica de base e., introducimos el paquete Legend que permite colocar leyendas a cada una de las funciones representadas.
También usaremos la opción PlotStyle que permite modificar el grosor, color y el aspecto de cada gráfica.
Needs["Graphics`Legend`"]
Plot[{x, Exp[x], Log[x]}, {x,-3,6}, PlotRange->{{-3,6}, {-2,6}},AxesLabel->{x,y}, PlotStyle>{{Thickness[0.01]},{Thickness[0.02], RGBColor[0.7,0,0]},{Thickness[0.02], RGBColor[0,0,1]}},LegendPosition->{1.1,0.2}, LegendSize->{1.5,0.5},AspectRatio->Automatic,
LegendSpacing->0.1, LegendShadow->{0,0},PlotLegend->{"Id(x)", "Exp(x)", "Log(x)"}]
El mismo gráfico se realizó con Derive
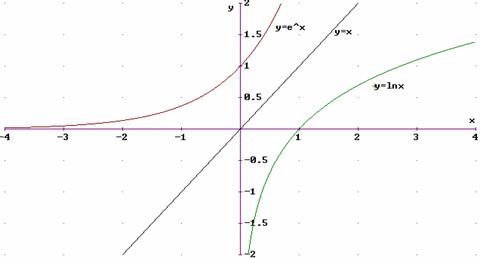
Resumiendo las funciones exponencial y logarítmica de iguales bases son inversas y sus gráficos son simétricos con respecto a f(x) = x.