|
|
| 1 2 3 4 5 |
Actividad integradora:
En este trabajo presentamos la solución de uno de los problemas propuestos, realizada con Mathematica y proponiendo a los alumnos la solución del mismo utilizando el software Derive.
Población de truchas. En un estanque grande se introducen mil truchas de un año de edad. Se espera que el número N(t) de las que viven todavía después de t años sea N(t) = 1000. 0.9t.
a) Tabular y graficar N(t) para 0 £ t £ 8
b) Estimar cuando habrá 500 truchas vivas
c) ¿Qué población de truchas viven entre 2 y 4 años?
a) Tabulamos y graficamos la función N(t) con las siguientes sentencias:
Table[1000*0.9^t, {t,0,8}]
Construye la siguiente lista:
{1000, 900., 810., 729., 656.1, 590.49, 531.441, 478.297, 430.467}
Plot[1000*0.9^t, {t, 0, 8}, AxesLabel->{X,Y}]
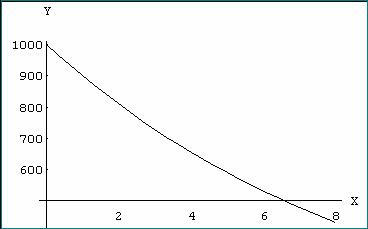
b) Igualando la función N(t) al valor dado de 500 truchas obtenemos una ecuación exponencial de variable t que resolvemos en Mathematica usando el comando NSolve
NSolve[1000*0.9^t==500, t]
Que al ejecutarlo resuelve numéricamente la ecuación planteada:
{{t -> 6.57881}}
El valor obtenido también lo podemos estimar a partir de los gráficos anteriores.
c) Calculamos N(2) y N(4) usando nuevamente el comando Solve
Solve[1000*0.9^2==N, N]
{{N -> 810.}}
Solve[1000*0.9^4==N, N]
{{N -> 656.1}}
Entonces la población de truchas entre 2 y 4 años disminuye de 810 a 656, como se observa en la tabla.
Consumo de agua. Un depósito suministra agua a una comunidad. Durante los meses de verano el consumo C(t) de agua en pies3/día, es :
![]()
en la cual t es el tiempo en días y t = 0 corresponde al inicio del verano.
a) Trazar la gráfica de C para 0 £ t £ 90.
b) ¿Cuándo es máximo el consumo de agua?.
CONCLUSIONES
Los docentes que elaboramos esta propuesta, que resultó positiva, consideramos que conlleva una serie de ajustes originados por distintos factores y que es viable implementarla con un mayor número de alumnos y otros temas de la asignatura.
Los recursos informáticos utilizados como herramienta ayudaron al enriquecimiento del campo per- ceptual y de las operaciones mentales involucradas en los procesos de construcción, estructuración y análisis de contenidos.
Esta experiencia permitió observar una buena disposición para el trabajo y el aprendizaje por parte de los alumnos a diferencia de una clase convencional, en la cual "aprendían" con una actitud exclusivamente receptiva.
BIBLIOGRAFÍA
1. Artigue, M. Douady, R. Moreno, L. Gómez, P. Ingeniería Didáctica en Educación Matemática. Un esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las matemáticas. Grupo Editorial Iberoamérica. Colombia. 1998.
2. Azcárate, C. Deulofeu, J. Funciones y Gráficas. Editorial Síntesis. España. 1990
3. Azinián, H. Resolución de Problemas Matemáticos. Visualización y manipulación con computadora.
Ediciones Novedades Educativas. Argentina. 1997.
4. Brousseau, Guy. Fondaments et méthodes fe la didactique. Recherches en didactique
des mathématiques 7.2. Versión en español publicada por F.a. M.A.F. Universidad Nacional
de Córdoba. 1987..
5. Chevallard, I; Bosch, M.; Gascon J. Estudiar Matemáticas. El eslabón perdido entre la enseñanza y
el aprendizaje. ICE-HORSORI. Universidad de Barcelona. 1997.
6. Larson, R; Hostetler, R; Edwards, B. Calculo y Geometría Analítica. Quinta Edición. McGraw-Hill.
España 1995.
7. Leithold, L. El Cálculo con Geometría Analítica. Sexta Edición. México.1992
8. Stewart, J. Cálculo de una variable. Trascendentes Tempranas. Tercera Edición International
Thomson Editores S.A. México. 1998.
9. Swokowski, E. Algebra y Trigonometría con Geometría Analítica. Grupo Editorial Iberoamericana.
México. 1996.