Esquemas del Concepto de Ecuación Diferencial Ordinaria en un Contexto Curricular Tradicional Martín Enrique Guerra
Cáceres Escuela de Matemática Facultad de Ciencias Naturales y MatemáticaUniversidad de El Salvador
|
|
|
Resumen El objetivo de este artículo es explorar con qué habilidades y/o conocimientos se quedan los estudiantes una vez que han concluido un curso tradicional de Ecuaciones Diferenciales Ordinarias y, asimismo, proporcionar argumentos a favor de una nueva perspectiva metodológica para la enseñanza y el aprendizaje de esta disciplina. En este sentido, se aplica una metodología de investigación cualitativa y se utiliza la noción de Esquema en el marco de la teoría APOS para describir y analizar las producciones de los estudiantes cuando se enfrentan a tareas que demandan dibujar las gráficas de las soluciones de algunos problemas de valor inicial. Así, los esquemas del concepto de ecuación diferencial se caracterizan por el predominio de estrategias algebraicas y algorítmicas, presencia de concepciones de acción y de proceso de los conceptos básicos del cálculo y de las ecuaciones diferenciales y, en consecuencia, ausencia de conocimientos y/o habilidades metacognitivas. Palabras clave: Esquema, ecuación diferencial ordinaria, currículo tradicional, métodos algebraicos y métodos cualitativos.
Introducción En este trabajo se describen, analizan, interpretan
y caracterizan las producciones escritas y orales de cuatro estudiantes de la
Licenciatura en Matemáticas de la Universidad de El Salvador en torno al
concepto de solución de una Ecuación Diferencial Ordinaria (EDO). Se presentan
algunos resultados experimentales relevantes acerca de los esquemas de este concepto que se generan en los estudiantes que
siguen un programa tradicional. Estos esquemas
pueden caracterizarse por: el predominio de un modo de pensamiento
algebraico y algorítmico, una concepción de acción y proceso de los conceptos
implicados restringidas al registro algebraico (función, derivada, ecuación
diferencial, solución de un problema de valor inicial) y profusión de conocimientos
procedimentales; también ausencia de conocimientos y habilidades
metacognitivas, es decir, conocimientos conceptuales y estrategias generales
que les permitan reflexionar y controlar sus cogniciones y producciones (como
resultados de esos procesos) a fin resolver de manera eficiente las tareas
propuestas (dibujar la gráfica de una solución de una EDO). De otra manera,
puede afirmarse que en los esquemas de estos estudiantes no se ha desarrollado
el sentido de los símbolos. Todo ello, evidentemente, permite poner en tela de
juicio tanto la creencia generalizada entre el profesorado en la superioridad
del enfoque algebraico frente al geométrico como el mismo currículo tradicional
del primer curso EDO, que pervive aún exclusivamente como la
continuación algebraica y algorítmica del cálculo diferencial e integral y
margina los métodos cualitativos y se despreocupa de las competencias que desarrollan los
estudiantes sometidos a ese enfoque tradicional. Por ejemplo,
se puede observar
en estos cursos de EDO que cuando se les pide a los
estudiantes que resuelvan el problema de valor inicial
Sin embargo, muchos tienen serias dificultades para
acceder a las propiedades cualitativas de y(x),
careciendo de una imagen gráfica para ella, a pesar de que esto puede deducirse
fácilmente de la EDO. Otros el único significado que atribuyen a la expresión
de y(x) se reduce a una mera fórmula
y, en el mejor de los casos, algunos llegan a afirmar que para calcular Por otra parte, ya no puede seguirse ignorando las
evidencias empíricas que señalan que aquellos estudiantes que son competentes
en el registro gráfico/geométrico, sacan mejor provecho de ambientes de
aprendizaje que usan las nuevas tecnologías. Por ejemplo, Chau y Pluvinage
(1999) reportan que universitarios de primer año que tienen éxito en las tareas
cualitativas de las ecuaciones diferenciales ordinarias sacan mejor provecho
del trabajo gráfico utilizando Derive que los alumnos que trabajan bien la
parte algebraica. Y agregan, que si bien es cierto que, los métodos
cualitativos se adquieren más difícilmente, presentan, desde el punto de vista
didáctico, el interés de favorecer la transferencia de conocimientos. Por otra
parte, los trabajos de investigación y de innovación curricular del proceso de
enseñanza y aprendizaje de las Ecuaciones Diferenciales Ordinarias (Artigue,
1989, 1992; Blanchard, 1994; Blanchard, Devaney y Hall, 1999; Devaney, 1995;
Hernández, 1994; Hubbard y West, 1991; Kallaher, 1999), entre otros, en los
que, haciendo un uso intensivo de la tecnología, se promueve la articulación de
los diferentes sistemas de representación semiótica[1]: algebraico, gráfico y numérico. Evidentemente, estas
perspectivas se deben a las razones fundamentales siguientes: a) la posibilidad
de realizar en un primer curso un estudio acorde con la epistemología de las
EDO, conjugando los aspectos cuantitativos y cualitativos y los procesos de
modelación matemática, b) la posibilidad
de contar en la clase de matemáticas con poderosas herramientas gráficas
y computacionales para representar y transformar el contenido matemático y promover
ambientes de aprendizaje interactivos, c) la convicción de que el conocimiento
matemático es como el invariante de múltiples representaciones y que, por
tanto, llegar a comprender un concepto matemático implica ser flexible en los
procesos de conversión entre diferentes sistemas de representación (Artigue,
1992; Dreyfus, 1994; Duval, 1993), y d) los resultados de muchas
investigaciones didácticas, por ejemplo, (Cooley y Trigueros, 2000;
Ferrini-Mundi y Graham, 1994; Hauk, Mason, Selden y Selden, 1999) que señalan
que limitar el proceso de enseñanza y aprendizaje del cálculo al registro
algebraico y algorítmico no garantiza la comprensión de los conceptos básicos y
que, por el contrario, se generan en los estudiantes esquemas y habilidades
demasiado rígidas, así como capacidades muy pobres para transferir sus
conocimientos más allá del contexto en el cual éstos se adquirieron,
impidiéndose así su progreso hacia niveles superiores de pensamiento.
1] Un sistema de representación semiótica es un sistema semiótico que permite las tres actividades cognitivas siguientes: formación de una representación identificable como una representación de un registro dado, tratamiento de esta representación, es decir, transformarla en el registro donde ha sido formada y conversión de dicha representación en otra representación de otro registro (Duval, 1993).
|
|
|
Revista
Virtual, Matemática Educación e Internet.
|
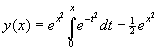, cuya sencillez es evidente, la gran mayoría son capaces de
obtener la solución siguiente 
.
sería necesario utilizar algún método de integración
numérica. Y están aquellos que no creen que tales expresiones sean respuestas
tan aceptables como aquellas en las que sólo aparecen funciones elementales
(evidenciándose así, dificultades con el Teorema Fundamental del Cálculo).