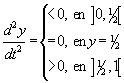|
|
|
Análisis
de Datos y Caracterización de los
Esquemas Para describir y
analizar las producciones de los estudiantes a las tareas propuestas, nos
preguntamos: ¿Qué estrategias se utilizan para dibujar la gráfica de una
solución de una EDO? ¿Cuáles son las dificultades encontradas? ¿Son los
estudiantes capaces de construir la gráfica de una solución derivando las
propiedades necesarias de dicha solución directamente de la EDO o, por el
contrario, primero sienten la necesidad de encontrar una fórmula para dicha
solución y posteriormente intentan dibujar su gráfica? Los resultados
obtenidos son reveladores: En
las respuestas dadas en los cuestionarios, todos los estudiantes muestran
claramente una tendencia dominante, en la cual no se toma en cuenta sí la
información relevante contenida en el lado derecho de la EDO está dada o bien
en el registro algebraico o bien en el gráfico. A saber: primero encontrar una
fórmula para la solución de la EDO utilizando el método de separación de
variables y luego intentar dibujar la gráfica de dicha solución utilizando las
técnicas del cálculo diferencial. Así, ninguno fue capaz de resolver eficientemente
las tareas propuestas, es decir, discriminar las propiedades relevantes de la
gráfica de la solución y coordinarlas con la información que proporciona la
ecuación diferencial para dibujar dicha gráfica. Tampoco, ninguno se dio cuenta
que la estrategia en cuestión es circular puesto que la primera derivada ya
está dada en la EDO o porque la estrategia podría ser poco fructífera debido a
que la fórmula obtenida podría resultar ser poco práctica para poder reproducir
eficientemente los esquemas previos del cálculo. De hecho, en las respuestas
del cuestionario a los problemas 2 y 4, dos estudiantes intentan integrar
formalmente ( I:…¿cómo graficaría
esta función? o ¿cómo haría la gráfica?. E1: Se mete esto en el Derive y…(risas). I: Exactamente, pero si no existiera el Derive, ¿cómo lo haría? E1: Si no existiera el Derive, le damos valores…pero no sé… I: Bueno, bueno…. ¿De qué otra manera podría graficar la función? E1: Ummm…ummm... E2: Entonces llego a esa solución. Y ahí no
la grafiqué pues…, intenté pero,… o sea como es un polinomio sexto, y así no
hallé cómo dibujarla. I: Sí, sí!. El procedimiento, esto, está
bien, usando separación de variables,… está bien. Pero lo que pedimos es el
gráfico de la curva solución. E2: Si, el gráfico, pero no lo hice. Y no lo
hice por eso, porque tengo un polinomio de grado sexto y así a mano… Los otros dos estudiantes, debido a errores
algebraicos, obtienen la expresión incorrecta
En la descripción anterior notamos que la ruta
cualitativa (resolver las tareas propuestas derivando directamente de la EDO la
información necesaria sin contar con una fórmula explícita para la solución) no
surge de manera natural y espontánea y, además, hay muchas dificultades
conceptuales y simbólicas para utilizar dichos esquemas algebraicos y
algorítmicos:¿Qué significa separar las variables? ¿Cuándo es pertinente
usarlo? ¿Cómo?. Esto nos lleva a realizar cuatro entrevistas semi-estructuradas
individuales para aclarar las respuestas dadas en el cuestionario e
intentar explorar el pensamiento de los
estudiantes cuando se les sugiere que resuelvan una EDO por métodos
cualitativos. Para esto, llegamos a los acuerdos siguientes: a) que para
dibujar la gráfica de la curva solución pedida pueden utilizar sus
conocimientos y técnicas del cálculo diferencial para derivar las propiedades
indispensables para construir dicha gráfica y b) dado que la primera derivada
ya está dada por la ED, no es necesario calcular explícitamente la fórmula de y(x). Sin embargo, el
pensamiento procedimental, algebraico y algorítmico, persiste con muchas
limitaciones e incoherencias. En efecto, todos se
mostraron estupefactos al considerar los ítems del cuestionario 3.2 y 4.2 en
los que se pedía encontrar I: ¿Qué tipo de punto es (-2, y(-2))? E2: Un máximo…pero, no estoy seguro de eso. I: ¿Cómo es un máximo? E2: Bueno, sería así Ç…alrededor de él la derivada pasa de positiva a negativa…pero aquí… va al revés, de negativa a positiva, entonces lo que tenemos es un mínimo. entonces hay un mínimo. I: Ujum! I: ¿Cómo sería el gráfico? Haga una propuesta
de gráfico. E2: Ummm…habría que analizar la concavidad
antes, no? I: Bueno, se podría analizar también. ¿Cómo
la analizarías? E2: Hay que derivar otra vez. I: Ujum, a ver derive. E2: Sería.…(después de 2 minutos):
Así verdad?, usando la regla de la cadena y
la derivada de un producto I: Ujum!, factorice. E2:…(después de 7 minutos):
… cómo que son irracionales las raíces, no? I: Eso parece. ¿Qué hay en los puntos (0,
y(0)) y (2, y(2))? E2:…ummm…son puntos de inflexión. I: Haga una propuesta de gráfico. E2:…ummm…(parece que no encuentra por donde
empezar a dibujar la gráfica). I: ¿Dónde hay cambios de concavidad? E2:…ummm… I: ¿Dónde dibujaría el mínimo (-2, y(-2))?
¿arriba o debajo de la recta y=1? E2:…ummm… I: ¿Podría haber cambio de concavidad en (-2,
y(-2))? E2:…ummm…(hay
un silencio largo) I: Sí, sí?. ¿Qué puede decir de la concavidad? E3:
Bueno…eee…sería necesario hallar la segunda derivada. I: Claro! o podríamos buscar algún otro tipo de argumento. Por ejemplo, sabiendo que la función es derivable, aquí en el mínimo no puede haber cambio de concavidad, porque de otra manera se formaría un pico. E3: Ummm…si, y no puede venir hacia abajo tampoco porque … es positiva siempre…. I: Igual aquí en el mínimo no puede ser cóncava hacia abajo a los dos lados porque se formaría un pico. E3: Ujum? I: Observe que los puntos E3:
…ummm… I:
Por ejemplo, entre 0 y 2. E3:
Ahí sí sería necesario encontrar la segunda derivada. I:
O bien usar algún argumento geométrico que nos evite los cálculos y nos diga
como es la gráfica. E3: …ummm…no se me ocurre como… Evidentemente, esta
necesidad fuerte de querer contar con una fórmula para poder aplicar sus
esquemas previos del cálculo, condición necesaria auto impuesta, refleja la
presencia de una concepción de acción y
proceso de los conceptos básicos del cálculo limitada a un sólo registro:
el registro algebraico - analítico. El problema 2, muestra la existencia de unos
conocimientos y/o habilidades muy pobres para relacionar una función y su
función derivada en los registros gráfico y algebraico. No obstante, después de
algunos intercambios con el entrevistador, logran derivar la información
suficiente sobre la monotonía, los extremos, puntos de inflexión y la
concavidad. Pero, al igual de lo que sucede en problema 1, en el momento de
construir la gráfica todos muestran dificultades para articular la información
cualitativa disponible sobre la función (ver anexo: dibujos a, c y d). En
particular, se observan dificultades para precisar la posición relativa de los
puntos En los problemas 3 y
4, retomando la experiencia de los
problemas 1 y 2, intentan obtener alguna información de la EDO. Pero enseguida
se bloquean. Así que el entrevistador les pide que recuerden y enuncien algún
teorema de existencia y unicidad. Y dado que ninguno lo
hizo, el entrevistador tuvo que enunciarlo y discutir su interpretación y
utilidad. Sólo entonces, tres estudiantes logran derivar la información
suficiente sobre la monotonía y la concavidad y dibujan la solución correcta
(ver anexo: dibujos e, g), observándose, eso sí, una tendencia muy fuerte a
rutinizar la estrategia de solución y ciertas dificultades conceptuales. En particular,
las estrategias usadas para leer e interpretar la gráfica de g(x) en el problema 2, provocan, que en
el problema 4, ciertas dificultades para obtener de f(y) la información cualitativa de y(t). Por ejemplo, en un primer momento, todos determinan las
regiones de monotonía en términos de la variable independiente t. Y un estudiante, leyendo la gráfica
de f(y) del problema 4, obtiene para el signo de la segunda
derivada de la solución de y(t) una
expresión que está en contradicción con el comportamiento monótono y asintótico
de dicha solución (ser decreciente y tener como asíntotas horizontales las
rectas y=1 y y=0). Esto se aprecia en los siguientes tres segmentos de
entrevista con un estudiante: I: A ver, no olvides que lo que pedimos es la gráfica. E4: Pues sí… Vamos a ver…puedo hacer todo lo que yo quiera aquí, verdad? I: Sí claro!, todo lo que quieras. E4: …creo que es I: Sí, sí, siempre que E4: Entonces en este plano yt lo que estoy formando es una
cosecante, no?, entre 0 y I: Si claro, está relacionada al comportamiento de la cosecante. E4: En I: ¿Por qué decís que son puntos de inflexión? E4: La derivada tiende a infinito, no! I: Pero… no necesariamente tienen que ser puntos de inflexión, no!! E4: Bueno, no necesariamente, tendría que analizarlo un poquito más...Ah!, ja, no necesariamente porque simplemente puede tender, nada más. Observemos que la inversión de la ecuación permite
tratarla como la ecuación del problema 2 en el plano yt . Pero, a la vez, aparecen dificultades conceptuales básicas
relacionadas con la derivada, las cuales se manifiestan reiteradamente. Veamos: E4: Lo que me tiene ahorita en líos es…Ah!, no, no, estoy pensando en otra cosa. Algo así diría yo…algo así (ver anexo: dibujo h). A menos que aparecieran otros puntos de inflexión, va!, que cambiara de curvatura en alguna otra parte de aquí. I: Pero, crees que hayan otros puntos de inflexión. ¿Cómo te aseguras de eso? E4: Creo que no, pues aquí en el gráfico no se refleja ningún otro. I: ¿Cómo lo ves? E4: Por la suavidad de la curva, no? I: Ujum! E4: No tiene ningún punto en la cual esté indefinido. I: Será por la suavidad u otra propiedad. E4: La continuidad, no! I: Ummm…¿Cómo se garantiza que no haya puntos de inflexión? E4: Estas hablándome de la solución, no de la derivada. I: Sí, del gráfico de la solución. Y lo que quiero que veas es que cuando crece no hace onditas. E4:
Es que creía que me decías que cómo
podía asegurarlo, pero yo lo miraba en la derivada, vaya!. Que la derivada
era.…- señalando el gráfico de la cosecante. I: Exactamente. Viendo esto – el gráfico de la cosecante- cómo aseguras que la solución no hace ondas. Crece pero no hace ondas. E4: ¿Cómo garantizo que aquí no hay puntos de inflexión?…no es que si habrían puntos de inflexión aquí – señalando la gráfica de la cosecante- aparecerían puntos en los que no estaría definida, no? I: Ummm… E4: Yo así lo creo. Los puntos de inflexión, forzosamente, se reflejarían en que no estaría definida la derivada, no?. Entonces habrían puntos en que la derivada no es continua, tendría pequeños saltitos. I: ¿De qué otra manera surgen los puntos de inflexión? E4: Bueno, básicamente un punto de inflexión surge donde no esté definida la derivada… En el problema 4, leyendo la gráfica de f(y) obtiene el signo de la segunda
derivada de la solución: E4: Bueno, agarro este pedazo,
Bueno, va! Entonces, como hemos
dicho que en ½ corta a y, y I: Sí, sí E4: tendríamos el mismo
comportamiento anterior, la función sería cóncava hacia arriba en I: Bueno, parecida. E4: Parecida me sale…Ah ja! f siempre es negativa…entonces tengo una función decreciente, no! I: Sí. E4: El punto de inflexión
lo tengo aquí en (0, 1/2), va! I: Ahora, hace la gráfica. E4:...ummm…sólo me aparece un punto de inflexión porque la segunda derivada solo se anula en ½, porque en ese pedazo f solo tiene una tangente horizontal. Pero…no pega!…¿qué está mal? Al cambiar las
condiciones iniciales y pedirles que dibujen las gráficas correspondientes, a
pesar de afirmar que los análisis y conclusiones obtenidos antes se conservan y
que lo único que cambia son las condiciones iniciales, todos producen dibujos
incoherentes, dibujando los puntos de inflexión en dichas condiciones iniciales
(ver anexo: dibujos f, g y h). Esto permitió rechazar la ilusión del
entrevistador de que la discusión y negociación de significados sostenida había
favorecido que los estudiantes asimilaran significativamente la ruta
cualitativa. Esto se muestra en los tres segmentos de entrevistas siguientes: I: Bien, ahora dibuje la solución
que pasa por el punto E3: Sería lo mismo siempre. Sólo
tendría que analizar los signos acá nuevamente de la primera y la segunda
derivada…ummm…siempre tengo que es creciente. También tengo que la segunda
derivada es positiva en I: Dibújela! E3: Tenia que era creciente,
cóncava hacia arriba en I: Haga una gráfica que Ud. crea que se aproxima. E3: Sería así… I: Ujum! …entonces el punto E3: Sí! I: Grafique ahora la solución que
pasa por E3: Sería lo mismo, siempre
(dibujando el punto de inflexión en I: Ahora gráfica la curva
solución que pasa por el punto E4: Yo la graficaría así….(ver gráfica de rojo en la figura anterior). I: Estas poniendo el punto de
inflexión en E4: Ah! No, no, si es cierto, el punto de inflexión estará aquí… I: ¿Dónde exactamente? E4: Esperate,…vamos a ver. Por tanto, la
información obtenida de los cuestionarios y de las entrevistas permite concluir
que en los esquemas del concepto de
EDO de los sujetos investigados se evoca, por una parte, sólo una expresión
algebraica en la que se relaciona una función, la variable independiente y su
derivada y, por otra, una noción de resolver una EDO que supone usar algún
método algebraico para encontrar una fórmula que satisfaga la ecuación
diferencial. Estos esquemas contienen
conexiones cognitivas muy débiles para: 1) leer, interpretar y tratar un
problema de valor inicial planteado en el registro gráfico y 2) coordinar los
registros gráficos y algebraicos para tratar con una función y sus derivadas
cuando éstas no se expresan mediante fórmulas explícitas. Asimismo, no existe
una red fuerte de relaciones gráficas e intuitivas que permita obtener ciertas
propiedades cualitativas (concavidad, puntos de inflexión, etc.) o, de manera
más general, dar argumentos y justificaciones en el registro gráfico a fin
dibujar la gráfica de los problemas de valor inicial propuestos. Por ejemplo,
la noción e imagen geométrica subyacente de extremo local limitada sólo a
puntos donde la función es derivable, aparece como un obstáculo para razonar en
el registro gráfico. También, existe una tendencia muy fuerte a
compartimentalizar y rutinizar los conocimientos y estrategias que exige la
ruta de solución cualitativa. Así pues, los esquemas se pueden caracterizar por: el predominio de un modo de pensamiento algebraico y algorítmico, una concepción de acción y proceso de los conceptos implicados (función, derivada, ecuación diferencial, solución de un problema de valor inicial) y profusión de conocimientos procedimentales; también ausencia de conocimientos y habilidades metacognitivas, es decir, conocimientos conceptuales y estrategias generales que les permitan reflexionar y controlar sus cogniciones y producciones (como resultados de esos procesos) a fin resolver de manera eficiente las tareas propuestas. De otra manera, podríamos decir que el nivel de desarrollo de estos esquemas está en un intra nivel operacional limitado a un solo registro. En fin, todo esto, en conjunto, permite caracterizar los esquemas como pobres, débiles, incoherentes y rígidos. Además, tales esquemas pueden ser considerados como un obstáculo para el modo de pensamiento y los conocimientos conceptuales que demanda la ruta cualitativa.
|
|
|
Revista
Virtual, Matemática Educación e Internet. |
ó
)
, pero no intentan graficarla ni dan señales de que hayan
intentado utilizar sus conocimientos del cálculo. Esto último se confirma en
los dos segmentos de las entrevistas siguientes:
, 
.
, debido a no contar a priori con una fórmula para la
solución y(t). Al abordar nuevamente
el problema 1, todos fueron capaces de derivar la monotonía y los extremos
analizando la expresión del lado derecho de la EDO. Pero, a pesar de que tal
análisis es evidente de la expresión algebraica, recurren a construir un cuadro
de variación. Además, la idea de extremo local se limita a un extremo en un
punto derivable. Y para decir algo de la concavidad, todos sienten la necesidad
de hallar la fórmula de la segunda derivada y no aceptan argumentos gráficos e
intuitivos basados en la suavidad de las soluciones. Esto se aprecia muy bien
en los dos siguientes segmentos de entrevistas con dos estudiantes en torno al
problema 1:
,
y 
, en el problema 1, y los puntos
,
y 
, en el problema 2 (donde M y m son las abscisas de los
puntos máximo y mínimo de g(x)
respectivamente).
, sí verdad?
.
. Ahora recordemos cómo se comporta la cosecante, y el
comportamiento de la cosecante
, y en ese… tendría que…Bueno llegaríamos a la misma
situación que antes, en 
,…
y cóncava hacia abajo en 
…entonces obtendríamos la misma solución de antes, no?
.
. Entonces la gráfica sería … 
y cóncava hacia abajo en 
. Entonces en este punto 
es un punto de inflexión.
.
).
.
.