Algunos usos de las calculadoras y la computadora para introducir el concepto de derivada
Alexander Borbón Alpízar
Estudiante de Maestría en Ciencias
Matemática Educativa, CINVESTAV del IPN
Resumen
Este artículo se basa en que las nuevas tecnologías representan una alternativa para la enseñanza y el aprendizaje de las matemáticas; las calculadoras simples, las calculadoras gráficas y las computadoras han ido desplazando a la tiza y a la pizarra, pues los temas pueden ser mostrados con mayor dinamismo y agilidad.
Sin embargo, un problema muy común entre los profesores es que cuentan con la tecnología para innovar, pero no saben como hacerlo, en el artículo se sugieren algunas formas de utilizar la tecnología para introducir el concepto de derivada, algunos modos de aproximarla y, por último, cómo obtener reglas generales.1.
Introducción
La utilización de nuevas tecnologías en el salón de clases trae consigo una nueva gama de posibilidades para la enseñanza-aprendizaje de las matemáticas. El uso de la tiza y la pizarra (aunque se seguirán utilizando por mucho tiempo) está siendo relegado por la introducción de calculadoras y computadoras. La principal razón es que estos instrumentos pueden mostrar, de forma dinámica, conceptos que son muy difíciles de enseñar de la forma tradicional.
Ya desde 1990 se ven los primeros intentos de introducir la tecnología en el aula, Jiménez (1990) y Scott (1990) muestran el impacto que estaban teniendo las computadoras y las calculadoras en esa época, afirman que las computadoras ya tenían un precio accesible y se estaban volviendo populares entre los matemáticos. También muestran el gran potencial que tiene esta tecnología para la enseñanza de temas como el cálculo, en donde se presentan conceptos abstractos, muchos de los cuales involucran procesos al infinito; en particular Jiménez muestra como utilizar una calculadora simple para encontrar el valor de algunas derivadas.
Actualmente el impacto de la computadora sigue de forma abrumadora, Díaz et al. (1997) apunta que “el uso de la tecnología en el salón de clases se ha convertido en una poderosa herramienta para una mejor comprensión y entendimiento de las matemáticas”; además el National Council of Teachers of Mathematics en 1998 señala que las actividades que permite la tecnología tales como visualizar, representar y formular relaciones matemáticas aparecen como centrales en el currículum matemático (citado en Santos et al., 1999).
Esto nos da una idea de la importancia que representa la utilización de la tecnología en la enseñanza-aprendizaje de las matemáticas, pues cuando se utilizan distintas representaciones de un objeto matemático en el aula se puede lograr que se transforme en algo “concreto” para el estudiante (algo que puede ver y manipular) en vez de un concepto inalcanzable para él.
Al ver todas las ventajas que presenta la tecnología es normal que los profesores y las profesoras quieran innovar en su salón de clases, sin embargo, un problema muy común que se presenta es que no se sabe qué actividades se pueden realizar para que se obtenga el mayor aprovechamiento; por eso introducir la tecnología al aula implica un mayor planeamiento de las clases y un buen dominio por parte del docente.
Para tratar de responder a esta iniciativa es que se sugieren algunas formas de utilizar la tecnología para la introducción del concepto de derivada, se inicia con un problema para motivar a los estudiantes y se ven distintas formas en que puede ser resuelto, para este problema se necesita que los estudiantes dominen algunos conceptos básicos de física tales como distancia, tiempo, velocidad, velocidad promedio y lectura de gráficas, sin embargo, si no los conocen se les puede explicar de forma sencilla antes de iniciar la actividad.
2.
Problema inicial para introducir la derivada
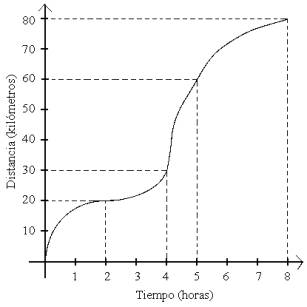
Cuando se introduce un nuevo concepto (en este caso la derivada) se debe buscar un problema o ejercicio que motive a los estudiantes a trabajar en él, buscar su solución y que ésta solución sea la definición que se les pretende dar. En este caso se va a introducir el concepto de derivada mediante un problema de física con un gráfico de distancia vs. tiempo, en un inicio no importará la función que se tome, lo importante será mostrar la noción de velocidad instantánea a partir de velocidades promedio (la idea de este ejemplo fue tomada de Novodvorsky, 1998), la explicación del problema es hecha primero por la profesora o el profesor hasta que quede claro.
Para la ubicación del problema primero se toma un gráfico de distancia contra tiempo y se calculan varias velocidades promedio, si algún estudiante no recuerda cómo calcular la velocidad promedio entonces se le puede explicar de una forma muy sencilla; le hacemos una pregunta como la que sigue: si usted viaja a un lugar que está a 50 kilómetros de distancia y duró 2 horas en el viaje, ¿a cuántos kilómetros por hora hizo el viaje?. Es casi seguro que el estudiante contestará que viajaba a 25 kilómetros por hora, ahora necesariamente se puede argumentar que el carro no viajó a una velocidad constante todo el viaje (seguro hizo alguna parada o a veces tubo que ir despacio y otras veces viajó más rápido), por lo que él va a llegar a la conclusión que los 25 kilómetros por hora es una velocidad promedio del viaje.
Así, la velocidad promedio puede ser definida por los mismos estudiantes como el valor que se obtiene al dividir la distancia recorrida entre el tiempo utilizado, se debe hacer notar que en un gráfico esto no es otra cosa que la pendiente de la recta secante que pasa por los puntos que se están evaluando.