4. Sugerencias Adicionales
Una vez que se ha introducido el concepto de derivada se pueden realizar varias actividades que puedan reforzarlo, además se pueden encontrar algunas reglas de la derivada al seguir procedimientos generales que se explican a continuación.
a. Visualización de la Recta Tangente
Una forma “intuitiva” de definir la derivada es como la pendiente de la recta tangente. Sin embargo, Llorens (1999) pone de manifiesto que los estudiantes no dominan o desconocen el significado de conceptos básicos como “curva”, “área”, “recta”, “tangente” y “punto”; las ideas “intuitivas” que tienen de estos conceptos muchas veces están en contradicción con su definición formal. Por esto se hace necesario mostrar, de una manera sencilla, qué es la recta tangente a una curva en un punto.
| La idea es mostrar el hecho de que una función localmente se comporta como una función “casi lineal” (Shultz, 1995), ya que si |
|
| entonces se puede aproximar f(x) como |
|
y si x es cercano a c entonces la función se comporta como “casi lineal”. |
Con la tecnología esta idea de ser
casi lineal puede tomar mucho sentido, si se grafica una función como
y se hacen varios
acercamientos al punto (1, 1) se verá cómo la función va tomando la
forma de una recta (Ver figura). La
línea que corresponda con esta amplificación es la recta tangente (Llorens,
1999; Shultz, 1995)).
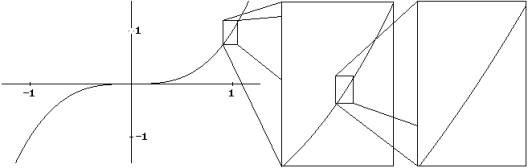
Si se grafica la función junto con la recta tangente lo que se percibe es que tienen muchos puntos en común, pero no hay contradicción con la definición estricta de recta tangente a una curva ya que ningún ordenador puede hacer infinitas ampliaciones a la gráfica en el punto (Llorens, 1999).
| Lo importante de este ejemplo es que se puede ver fácilmente los casos en los que la derivada no existe, como |
|
ó |
|
cuando |
|
, pues |
| (por más aproximaciones que se hagan) la primera siempre se verá como un pico y la segunda es oscilante (nunca se verá como una recta). | ||||||
Cuando se introduce la recta tangente de esta forma se puede enseñar la derivada simplemente como la pendiente de lo que aparenta ser una recta al acercarse (hacer zoom) al punto (c, f(c)) (Shultz, 1995).
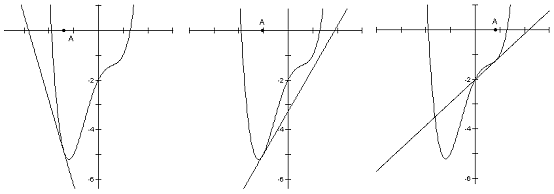
Otra forma de visualizar la recta tangente es con el
programa Sketchpad, se puede graficar una función y la recta tangente en
un punto cualquiera (en Sketchpad es sencillo pues se puede calcular la
derivada de una función), al mover el punto por la gráfica se puede ver
como cambia la recta tangente y los problemas que se puede tener en
funciones con picos o oscilatorias. En la figura se muestra la recta
tangente al gráfico cuando se mueve el punto A.
Una vez que se maneja el concepto de “recta tangente” es momento de iniciar la exploración sobre el cálculo de la derivada.
b.
Cálculo de la derivada de
Novodvorsky (1998) expone una excelente idea para descubrir la regla de la derivada de una potencia al trabajar con los estudiantes; se les da cinco monomios, todos de distinto grado, se les pide que calculen la pendiente de la recta tangente en varios puntos, con estos valores se puede hacer una conjetura sobre la derivada del monomio o se puede realizar la gráfica de una función que pase por los puntos calculados (esto es inmediato en un programa como Graphical Analysis III software package) y luego se encuentra la función de este gráfico.
Como ejemplo, trabajaron con el
monomio
, al graficar los puntos observaron que el gráfico parecía ser el de una
función cúbica, así que graficaron los puntos vs.
(hicieron la sustitución
), al ver que el gráfico era una línea recta concluyeron que la derivada
sí es una cúbica y al ver que la línea era v = 8u
entonces la cúbica es
. Por lo tanto la derivada de
es
.
Al hacer el proceso para los cinco
monomios se encuentra el patrón general y se llega fácilmente a que si
entonces
.
Otra forma de calcularlo es utilizar la calculadora gráfica o la computadora para realizar la derivación simbólica y así inferir la regla general, la idea es utilizar el programa al revés, lo que se hará es calcular la derivada de forma directa para algunas funciones y luego se hará la generalización, veamos otra vez el ejemplo de los monomios, se realizan las siguientes tablas
|
Para la fórmula general se tiene
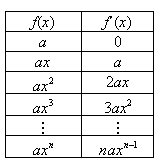
Por lo que la fórmula general es:
si
entonces
.
Este mismo proceso se puede utilizar para “descubrir” otras fórmulas de derivadas.