3.  Métodos para encontrar la velocidad instantánea

Como mencionamos en la sección anterior, se pueden utilizar distintos métodos para encontrar la velocidad instantánea de un automóvil teniendo la gráfica o la función de la distancia contra el tiempo, en esta sección se explicarán a detalle estos métodos.  De ahora en adelante no se hablará de la velocidad instantánea sino que ya se utilizará el término de la derivada de una función en un punto.

a.      Secantes Próximas

Este método tiene dos fines importantes: el primero es aproximar la derivada de una función en un punto y el segundo es mostrar la idea de aproximarse por medio de secantes a la tangente para que sea más sencillo a la hora de dar la definición de derivada como el valor al que tiende la pendiente de las secantes conforme t tiende a cero.

Si solo se cuenta con calculadoras simples entonces será necesario llevar las funciones previamente graficadas (preferiblemente hechas en computadora) para que los estudiantes trabajen con ellas (cada estudiante debe tener todas las gráficas que se van a utilizar).  Otra forma es que los estudiantes realicen las gráficas primero, pero esto consume mucho tiempo y lo más probable es que no queden muy bien.

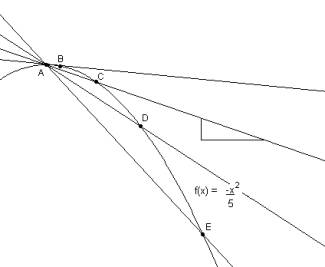
Ahora se les pide que realicen varias secantes a la gráfica, estas secantes deben pasar por el punto (c, f(c)) (en el caso del primer problema por 

(4, 30)) y por cualquier otro punto de la gráfica, al inicio deben tomar puntos alejados de (c, f(c)) y luego tomar valores cada vez más cercanos.  Cada vez que realicen una secante deben calcular su pendiente, para esto pueden tomar dos puntos que pertenezcan a la secante o formar un triángulo (como se

Con la calculadora gráfica se puede seguir un procedimiento similar, pero se tiene la gran ventaja que las gráficas se pueden realizar en la misma clase (esto le quita el trabajo al profesor de llevarle las gráficas a sus estudiantes), son gráficas confiables, se puede trabajar con acercamientos y con el cursor se puede aproximar dos puntos que pertenezcan a la gráfica de manera sencilla.

Se puede trabajar igual con la computadora; sin embargo, un programa como Geometer Sketchpad puede hacerlo todavía más sencillo: se grafica la función directamente, se grafica el punto (c, f(c)) (esto se hace directamente en Sketchpad), se construye la recta que pasa por ese punto y cualquier otro punto de la gráfica, el programa puede calcular la pendiente de esa recta, luego se trata simplemente de mover el segundo punto hacia el primero y observar qué sucede con la pendiente (hacia qué valor se aproxima).

b.      La Pendiente de la Recta Tangente al Gráfico

Este método de calcular la derivada es similar al anterior; si sólo se tienen calculadoras simples el profesor debe llevar las gráficas hechas, los estudiantes deben dibujar la tangente a la gráfica en el punto deseado (tan bien como se pueda) y luego calcular su pendiente, con esto se hace la conjetura.

Con calculadoras gráficas se puede realizar el gráfico en clase con mayor precisión y tiene la opción de graficar la recta tangente al gráfico en un punto, por lo que se esta seguro que la recta esta bien graficada (en la figura se ve graficada la función  junto con la recta tangente en el punto (1, 1)).

La computadora también presenta estas ventajas con la mejora que los gráficos son más finos.

c.      Dos Valores Cercanos

Para este método se deben tomar dos valores de la función muy cercanos al punto (c, f(c)) que es en donde se quiere encontrar la derivada, se puede tomar una diferencia entre las preimágenes de 0.01 (t = 0.01) y uno de los puntos puede ser el mismo (c, f(c)).

Así, por ejemplo, se puede hacer una aproximación de la derivada de la función  en el punto (1,1), al evaluar en la calculadora se obtiene que 

f(1.01)=1.030301, así

    d.     Manipulación Numérica y Simbólica del Límite

Para este método ya se debe haber “descubierto” la derivada como el límite		; lo que se hará es calcular este límite de manera
numérica con la calculadora simple (por aproximaciones) o de manera simbólica y sustituyendo con cualquiera de las tres tecnologías.

Como ejemplo, calculemos la derivada de

en el punto (1, 3), empecemos realizando una tabla del límite cuando nos acercamos a 0;

el límite es

Se puede hacer la conjetura que f '(1) = 9.

La otra forma es calcular directamente el límite

Con las calculadoras gráficas y las computadoras se puede calcular este límite directamente (si calcular el límite no es el objetivo sino encontrar la derivada).

También se puede encontrar la fórmula general de la derivada con el		(se podría calcular de forma directa con la calculadora gráfica y la
computadora); una vez que se tiene la fórmula general se evalúa el valor de c para encontrar la derivada de la función en el punto (c, f(c)).

Revista Virtual Matemática, Educación e Internet

Derechos Reservados