|
Desarrollo de la Propuesta
Iniciamos este trabajo recordando la manera de hallar la distancia entre dos
puntos
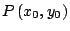 y y
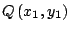 en un
sistema de coordenadas rectangulares. Consideremos los puntos en un
sistema de coordenadas rectangulares. Consideremos los puntos 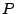 y y 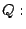
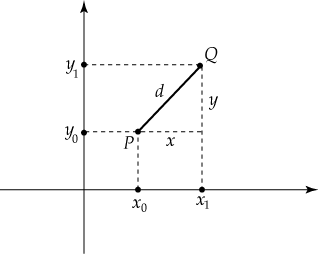
Nos interesa encontrar la longitud 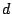 . Por el teorema de Pitágoras es
fácilmente observable en la figura 1 que: . Por el teorema de Pitágoras es
fácilmente observable en la figura 1 que:
El problema que nos interesa resolver, consiste en encontrar la distancia 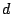 de un punto dado del plano cartesiano a una recta. Para ello consideremos un
punto
de un punto dado del plano cartesiano a una recta. Para ello consideremos un
punto 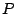 del plano, del plano, 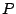 de coordenadas de coordenadas
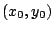 y la
recta y la
recta 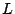 de ecuación asociada de ecuación asociada 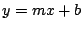 . Debemos encontrar la distancia
de . Debemos encontrar la distancia
de 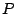 a la recta a la recta 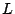 , por definición dicha distancia
corresponde a la longitud del segmento perpendicular a , por definición dicha distancia
corresponde a la longitud del segmento perpendicular a 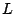 con extremo con extremo 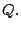 Obsérvese la siguiente figura:
Obsérvese la siguiente figura:
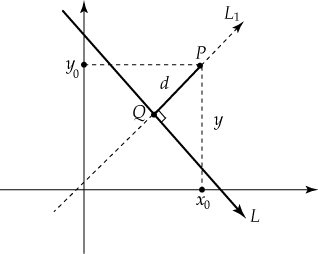
Si conociéramos las coordenadas de 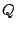 nuestro problema quedaría
completamente resuelto, pues nuestro problema quedaría
completamente resuelto, pues 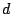 correspondería a la distancia entre correspondería a la distancia entre 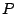 y y
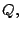 que la podemos determinar mediante la expresión que la podemos determinar mediante la expresión
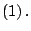 Hallemos estas coordenadas. Hallemos estas coordenadas.
Supongamos que 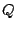 es de coordenadas es de coordenadas
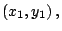 de
acuerdo a la figura 2 se puede concluir que de
acuerdo a la figura 2 se puede concluir que
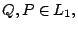 hallemos la ecuación asociada a esta recta.
hallemos la ecuación asociada a esta recta.
- Pendiente de
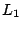
- La ecuación de
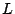 corresponde a corresponde a 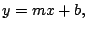 como como
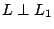 tenemos que:
tenemos que:
- Intersección con el eje de las ordenadas
- Como
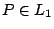 se tiene que: se tiene que:
- finalmente la ecuación asociada a
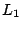 es: es:
Como 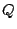 es un punto tanto de es un punto tanto de 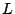 como de como de 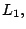 sus coordenadas satisfacen
las ecuaciones asociadas a ambas rectas, de donde: sus coordenadas satisfacen
las ecuaciones asociadas a ambas rectas, de donde:
entonces
Quedando de esta forma determinadas las coordenadas de 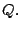 Luego, por Luego, por
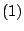 la distancia la distancia 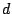 viene dada por: viene dada por:
donde
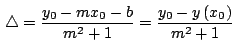 y y
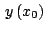 representa la ecuación de la
recta representa la ecuación de la
recta 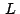 evaluada en evaluada en
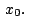
En conclusión, la distancia 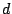 del punto del punto 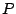 de coordenadas de coordenadas
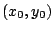 a la recta a la recta 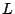 de ecuación asociada de ecuación asociada 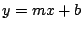 ,
corresponde a: ,
corresponde a:
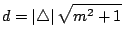 con: 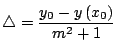
El resultado clásico que aparece en los libros de álgebra lineal para
resolver este problema, establece que:
con 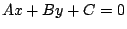 la ecuación general de la recta. la ecuación general de la recta.
Note que ambos resultados son equivalentes y no conducen a ningún tipo de
contradicción, pues cualquiera de ellos se puede inferir del otro.
Lo importante de la demostración que hemos explicado, es que no requiere
de ningún conocimiento de álgebra lineal para su desarrollo, por el
contrario, únicamente se fundamenta en algunos conceptos de matemática
básica.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|
![\begin{displaymath}
\begin{array}[c]{rcl}
\dfrac{-x_{1}+my_{0}+x_{0}}{m}&=&mx_{1...
...: }y_{1}&=&\dfrac{m^{2}y_{0}+mx_{0}+b}{m^{2}+1}\\
\end{array}\end{displaymath}](img38.gif)
![\begin{displaymath}%%
\begin{array}[c]{rcl}%%
d&=&\sqrt{\left( x_{0}-\dfrac{m\le...
...\left\vert \triangle
\right\vert \sqrt{m^{2}+1}\\
\end{array}\end{displaymath}](img42.gif)
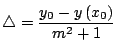
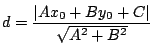

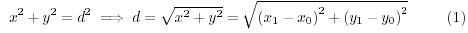

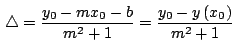 y
y