|
Ejemplos de Aplicación
- Determine la distancia del punto
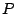 de coordenadas de coordenadas
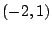 a la recta a la recta 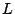 de ecuación asociada de ecuación asociada 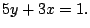
Solución
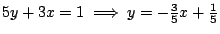
Luego:
Finalmente:
- Halle la distancia entre las rectas paralelas:
Solución
Por definición, esta distancia 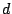 corresponde a la longitud
del segmento perpendicular de un punto cualquiera de ellas a la otra recta.
De esta forma, hallemos las coordenadas de un punto corresponde a la longitud
del segmento perpendicular de un punto cualquiera de ellas a la otra recta.
De esta forma, hallemos las coordenadas de un punto 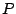 de de 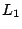 y
posteriormente calculemos la distancia de y
posteriormente calculemos la distancia de 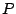 a a 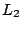 . .
Para 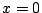 en en
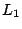 se obtiene se obtiene
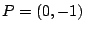 , luego: , luego:
En consecuencia:
- Determine las coordenadas de un punto
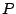 cuya distancia a la recta cuya distancia a la recta 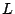 de ecuación asociada de ecuación asociada
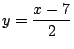 corresponde a corresponde a 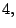 y represente
geométricamente el conjunto de todos los puntos del plano que satisfacen
esta condición. y represente
geométricamente el conjunto de todos los puntos del plano que satisfacen
esta condición.
Solución
Sea
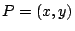 entonces: entonces:
de donde
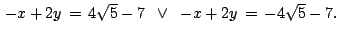
Ambas ecuaciones representan las ecuaciones asociadas a dos rectas paralelas
que llamaremos 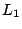 y y 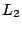 respectivamente, cualquier punto de las
rectas es una solución. Si en la ecuación de respectivamente, cualquier punto de las
rectas es una solución. Si en la ecuación de 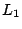 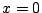 entonces entonces
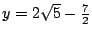 y el punto y el punto
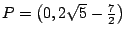 satisface la condición deseada. Geométricamente las
rectas paralelas satisface la condición deseada. Geométricamente las
rectas paralelas 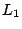 y y 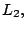 y la recta y la recta 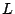 , vienen dadas por la
siguiente figura: , vienen dadas por la
siguiente figura:
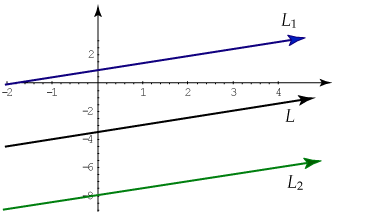
La recta de color azul corresponde a 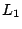 , la de color negro a , la de color negro a 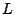 y la de
color verde a y la de
color verde a 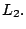
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|