
|

|
Suponga que
![]() son
son ![]() números positivos. Sea
números positivos. Sea
![]() un reordenamiento arbitrario de los
un reordenamiento arbitrario de los
![]() , entonces
, entonces
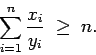 |
(1) |
| (2) |
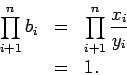
La demostración del teorema 1 puede encontrarse en [1] o bien intentarla por inducción. Sin embargo, la demostración de la desigualdad (1) puede también ser obtenida como un caso particular de una desigualdad estudiada por Hardy y Litlewood en los años 30. En la siguiente sección se estudiará tal desigualdad.
Revista digital Matemática, Educación e Internet.
Derechos Reservados