Reordenamiento

| José Rosales O | Pedro Díaz N.  | Revista Digital Matemática, Educación e Internet |

 

1 2 3 4 5 6

 

Ordenamiento de conjuntos

 

Supongamos que $X = \{x_1,x_2,\ldots,x_n\}$ y $Y=\{y_1,y_2,\ldots,y_n \}$ son dos conjuntos de números reales. Consideremos la siguiente expresión

$$x_1y_1\,+\,x_2y_2\, +\, \cdots \, +\, x_ny_n$$ (3)

Nos proponemos responder a la pregunta: ¿bajo qué condiciones sobre $X$ y $Y$ podemos concluir que (3) alcanza el valor máximo y el mínimo? El siguiente teorema responde esta pregunta.

Teorema 2   Sean $x_1\leq x_2 \leq \cdots \leq x_n$ y $y_1 \leq y_2 \leq \cdots \leq y_n$ números reales. Para cualquier permutación $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ de $(x_1,x_2,\ldots,x_n)$ se tiene que

$$\begin{eqnarray*} x_1y_1\,+\,x_2y_2\, +\, \cdots \, +\, x_ny_n & \geq & x_1^\pri... ... & \geq & x_ny_1\, +\, x_{n-1}y_2\, +\, \cdots \, + \, x_1y_n. \end{eqnarray*}$$

con igualdad si y solamente si $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ es igual a $(x_1,x_2,\ldots,x_n)$.

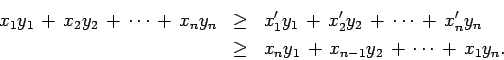
La demostración de este resultado se basa en lo siguiente. Supongamos, para empezar, que $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ es una permutación de $(x_1,x_2,\ldots,x_n)$ en la cual solamente se han intercambiado dos elementos. En tal caso existirán dos enteros $j$ y $k$, con $j < k$, tales que

• $y_j \leq y_k$,
• $x_j^\prime > x_k^\prime$.

Como

$$\begin{eqnarray*} y_jx_k^\prime \, +\, y_kx_j^\prime \, -\, (y_jx_j^\prime \,+\,... ...prime) & = & (y_k -y_j)(x_j^\prime - x_k^\prime)\\ & \geq & 0, \end{eqnarray*}$$

se sigue que

$$y_jx_k^\prime \, +\, y_kx_j^\prime \; \geq \; y_jx_j^\prime \,+\, y_kx_k^\prime$$

Teniendo presente que $x_k^\prime = x_j$ y que $x_j^\prime = x_k$, hemos demostrado que

$$y_jx_j \, +\, y_kx_k \; \geq \; y_jx_j^\prime \,+\, y_kx_k^\prime$$

Esto demuestra la validez del teorema en el caso en que $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ es una permutación de $(x_1,x_2,\ldots,x_n)$ en la cual solamente se han intercambiado dos elementos. El caso general se sigue del anterior al aplicar el resultado un número finito de veces.

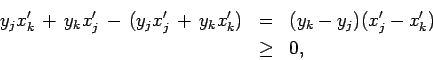
Si analizamos la demostración anterior nos percataremos que en el fondo lo que hicimos fue partir de un conjunto ordenado, luego lo desordenamos y nuestro procedimiento nos lo reordena. Observe también que el teorema (2) se utiliza para cualquier tipo de números, no importa si son positivos o negativos. Esto representa una enorme ventaja con respecto a la mayoría de las desigualdades conocidas.

Los siguientes corolarios son muy importantes. De hecho, el corolario (2) no es nada más y nada menos que el teorema 1. En el año de 1935 un problema del examen Kurschak de Hungría pedía la prueba del corolario (2).

Corolario 1   Sea $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ una permutación de $(x_1,x_2,\ldots,x_n)$ ,entonces se cumple que

$$x_1^2\,+ \, x_2^2 \, + \, \cdots\, +\, x_n^2 \, \geq \, x_1x_1^\prime\, +\, x_2x_2^\prime\, +\, \cdots \, + \, x_nx_n^\prime$$

Corolario 2   Sea $(x_1^\prime,x_2^\prime,\ldots,x_n^\prime)$ una permutación de $(x_1,x_2,\ldots,x_n)$ ,entonces se cumple que

$$\frac{x_1^\prime}{x_1}\,+ \,\frac{ x_2^\prime}{x_2} \, + \, \cdots\, +\, \frac{x_n^\prime}{x_n} \, \geq \, n.$$

1 2 3 4 5 6

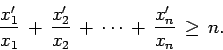
Revista digital Matemática, Educación e Internet.
Derechos Reservados