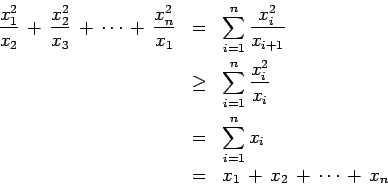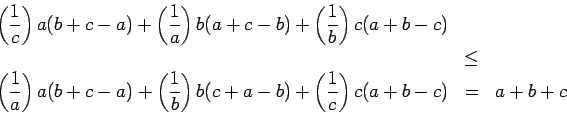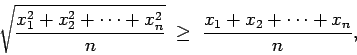- Ejemplo 1
- Sean
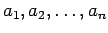 números positivos. Entonces
números positivos. Entonces
![\begin{displaymath}
\sqrt[n]{a_1\cdot a_2\cdots a_n} \; \leq \; \frac{a_1\,+\,a_2\,+\, \cdots\, +\,a_n}{n}
\end{displaymath}](img32.gif) |
(4) |
con igualdad si y solamente si
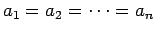 .
La desigualdad (4) es la famosa desigualdad de la media geométrica y la media aritmética. Para deducirla a partir del corolario (2) hagamos lo siguiente. Sea
.
La desigualdad (4) es la famosa desigualdad de la media geométrica y la media aritmética. Para deducirla a partir del corolario (2) hagamos lo siguiente. Sea
![$ G =\sqrt[n]{a_1\cdot a_2\cdots a_n}$](img34.gif) , luego tomemos
, luego tomemos
y apliquemos el teorema (1), que es en realidad un corolario del teorema (2), para obtener
lo cual es equivalente a que
- Ejemplo 2
- Sean
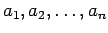 números positivos. Entonces
números positivos. Entonces
![\begin{displaymath}
\sqrt[n]{a_1\cdot a_2\cdots a_n} \; \geq \; \frac{n}{\frac{1}{a_1}\, +\,\frac{1}{a_2}\, +\, \cdots \, +\, \frac{1}{a_n} },
\end{displaymath}](img37.gif) |
(5) |
con igualdad si y solamente
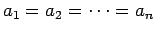 .
La desigualdad (5) se conoce como la desigualdad de la media geométrica y de la media armónica. Para demostrarla sean
.
La desigualdad (5) se conoce como la desigualdad de la media geométrica y de la media armónica. Para demostrarla sean 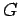 y
y
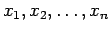 como en el ejemplo anterior, entonces aplicando el teorema (1), se sigue que
como en el ejemplo anterior, entonces aplicando el teorema (1), se sigue que
lo cual es equivalente a
con igualdad si y solamente
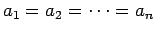 .
.
- Ejemplo 3
- Sean
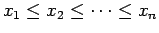 y
y
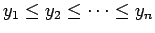 números reales. Entonces
números reales. Entonces
con igualdad si y solamente si para alguna constante 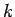 , se tiene que
, se tiene que 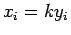 para
para
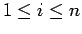 .
.
La desigualdad anterior es la famosa desigualdad de Cauchy-Schwarz. Para su demostración observe que si
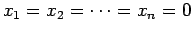 ó
ó
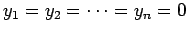 , entonces el resultado es trivial. De otra forma, sea
, entonces el resultado es trivial. De otra forma, sea
 y
y
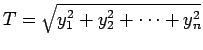 . Definamos
. Definamos 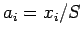 y
y
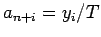 , para
, para
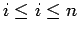 . Por el corolario 1, se sigue que,
. Por el corolario 1, se sigue que,
lo cual es equivalente al resultado deseado. Igualdad se obtiene si y solamente si 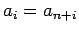 para
para
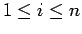 , o lo que es lo mismo,
, o lo que es lo mismo, 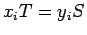 , para
, para
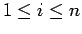 .
.
- Ejemplo 4
- Este ejemplo apareció como la primer pregunta de la Olimpiada Internacional de 1975, cuya sede fue Bulgaria. Sean
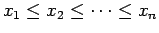 y
y
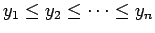 números reales. Sea
números reales. Sea
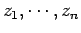 una permutación arbitraria de los
una permutación arbitraria de los
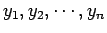 . Demuestre que
. Demuestre que
La solución oficial es sumamente extensa, el lector puede comprobarla al ver [2] que es de donde nació la idea de este artículo. Sin embargo, si usamos el teorema 2 la solución es inmediata. En efecto, si desarrollamos la expresiones del lado izquierdo y del lado derecho de la desigualdad anterior, obtenemos
Teniendo en cuenta que
se concluye que
que es precisamente el teorema 2.
- Ejemplo 5
- Este ejemplo apareció como la quinta pregunta de la Olimpiada Internacional de 1978, cuya sede fue Rumania. Sean
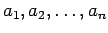
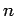 enteros positivos distintos. Pruebe que se cumple que
enteros positivos distintos. Pruebe que se cumple que
Sea
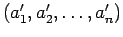 una permutación de términos crecientes de
una permutación de términos crecientes de
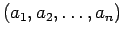 , es decir que
, es decir que
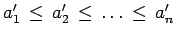 . Observe que al ser los
. Observe que al ser los 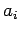 enteros positivos y diferentes, se concluye que
enteros positivos y diferentes, se concluye que
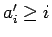 , para
, para
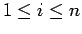 . Usando el teorema 2 se concluye que
. Usando el teorema 2 se concluye que
- Ejemplo 6
- El siguiente problema apareció en una competencia de la República Popular de China, correspondiente al año 1985. Pruebe que
para todos los números positivos
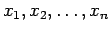 .
.
Si tomamos 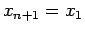 , entonces el lado derecho de la desigualdad anterior toma la siguiente forma al usar sumatorias
, entonces el lado derecho de la desigualdad anterior toma la siguiente forma al usar sumatorias
- Ejemplo 7
- Este ejemplo apareció como la quinta pregunta de la Olimpiada Internacional de 1983, cuya sede fue Francia. Sean
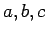 los lados de un triángulo. Pruebe que
los lados de un triángulo. Pruebe que
Sin pérdida de generalidad podemos asumir que
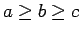 . En primer lugar probaremos que se cumple que
. En primer lugar probaremos que se cumple que
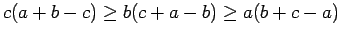 . En efecto, observe que
. En efecto, observe que
La otra desigualdad se prueba en forma totalmente análoga. Ahora, usando el teorema 2, se sigue que
Simplificando, obtenemos que
la cual es equivalente a la desigualdad original. El mismo argumento se aplica si se supone que
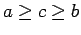 .
.
Para finalizar se dejan, como ejercicio, los siguientes ejemplos
- Ejemplo 8
- El siguiente problema apareció en una competencia de la ciudad de Moscú, correspondiente al año 1963. Pruebe que
suponiendo que 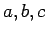 son números positivos.
son números positivos.
- Ejemplo 9
- Sean
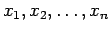 números reales. Entonces
números reales. Entonces
con igualdad si y solamente si
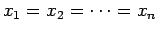 .
.
- Ejemplo 10
- El siguiente problema apareció en la Olimpiada Internacional de Matemática del año de 1964. Sean
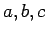 los lados de un triángulo. Pruebe que
los lados de un triángulo. Pruebe que


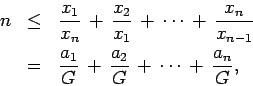
![\begin{displaymath}
\sqrt[n]{a_1\cdot a_2\cdots a_n} \; \geq \; \frac{n}{\frac{1}{a_1}\, +\,\frac{1}{a_2}\, +\, \cdots \, +\, \frac{1}{a_n} },
\end{displaymath}](img37.gif)
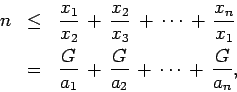
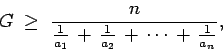
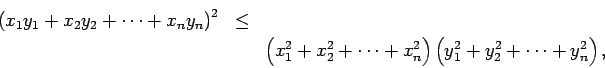
![]() ó
ó
![]() , entonces el resultado es trivial. De otra forma, sea
, entonces el resultado es trivial. De otra forma, sea
 y
y
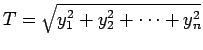 . Definamos
. Definamos ![]() y
y
![]() , para
, para
![]() . Por el corolario 1, se sigue que,
. Por el corolario 1, se sigue que,
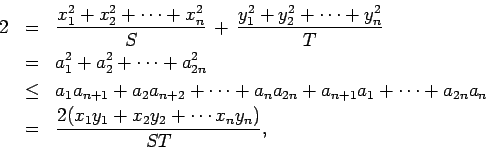
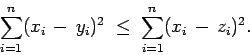
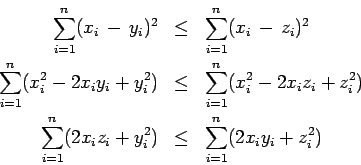
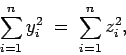
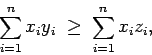
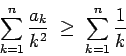
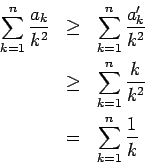
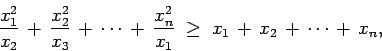
![]() , entonces el lado derecho de la desigualdad anterior toma la siguiente forma al usar sumatorias
, entonces el lado derecho de la desigualdad anterior toma la siguiente forma al usar sumatorias