Ejemplos

Ejemplo 1. Cuál es el número mínimo de personas que debemos reunir para asegurarnos que hay dos de ellas que cumplen años en el mismo mes?

Para usar el principio de Dirichlet debemos decir qué representan las perlas y qué representan las cajas. En este caso las perlas son la cantidad mínima de personas y las cajas representan los meses del año. No es difícil convencerse que 13 es el número mínimo de personas, ya que con este número se aplica de inmediato el principio de Dirichlet.

Ejemplo 2. Una prueba de concurso posee 10 preguntas de seleción múltiple, con cinco alternativas cada una. Cuál debe ser el mínimo número de candidatos para el cual podamos garantizar que por lo menos dos de ellos tendrán exactamente las mismas respuestas para todas las preguntas?

En este caso tenemos que los alumnos representan las perlas y las cajas son representadas por las posibles sucesiones de respuestas. Como cada pregunta puede ser respondida de 5 formas distintas, tenemos que la prueba puede ser respondida de 5×5×^...×5 = 5¹⁰ = 9 765 625 formas diferentes. Luego, para tener certeza de que por lo menos dos estudiantes van a tener las mismas respuestas, deben haber, por lo menos, 9 765 626 estudiantes.

Ejemplo 3. En una reunión hay n personas. Muestre que existen dos personas que conocen exactamente al mismo número de otros participantes (admitimos que ``conocer" es una relación de simétrica, es decir que, si a conoce a b, entonces b conoce a a).

Las perlas en este caso son las n personas. Las cajas, naturalmente, son las cantidades de personas conocidas. Tenemos una dificultad: las posibles cantidades de conocidos son 0, 1, 2,..., n - 1, luego a primera vista tenemos n perlas y n objetos, y por lo tnato no se puede aplicar el principio de Dirichlet. Lo importante en este ejemplo es notar que las posibilidades de conocer a 0 y a n - 1 personas no se pueden dar simultáneamente: si existe una persona que no conoce a ningún participante, entonces no puede existir una persona que conozca a todos los participantes. Así, una de las cajas 0 ó n - 1 permanece desocupada y las n perlas deben ser, por lo tanto, distribuidas entre las n - 1 cajas. Por lo tanto, habrá una de ellas que será ocupada por dos perlas, lo que muestra que existen dos personas que conocen al mismo número de participantes.

El siguiente problema tiene una historia muy interesante. Según cuenta el famoso Paul Erdös (ver [1]), este problema se lo propuso a Pósa, cuando este tenía tan sólo 12 anõs de edad, durante un almuerzo. Pósa lo resolvió en un abrir y cerrar de ojos.

Ejemplo 4. Entre n + 1 elementos del conjunto {1, 2,..., 2n} existen dos que son primos relativos.

La solución a este problema se puede hacer por medio del principio de Dirichlet. Sin embargo, en este caso no es muy obvio qué representan las perlas y qué representan las cajas. Esta escogencia, para este problema particular, es muy ingeniosa. La perlas representan los n + 1 números que se eligen del conjunto {1, 2,..., 2n}, y las cajas se eligen como los n pares de números consecutivos (1, 2), (3, 4), ..., (2n - 1, n). Luego, por el principio de Dirichlet, dos de los n + 1 números que elegimos quedarán en una misma caja, es decir, que estos dos números son consecutivos. Esto todavía no resuelve el problema original, el cual establece que hay dos números que son primos relativos, pero es conocido que dos números naturales consecutivos son primos relativos. Esto concluye la demostración del enunciado.

El siguiente ejemplo muestra la utilidad del principio de Dirichlet en algunos problemas de naturaleza geométrica.

Ejemplo 5. Considere cinco puntos P₁, P₂,..., P₅ en el interior de un cuadrado S de lado 1. Denote por d_{i, j} la distancia entre dos puntos P_i y P_j. Pruebe que al menos una de las distancias d_{i, j} es menor que $\sqrt{2}$ /2.

Divida a S en cuatro cuadrados congruentes como muestra la siguiente figura.

Por el principio de Dirichlet, dos puntos pertencen a uno de estos cuatro cuadrados ( un punto de la frontera de dos de los cuadradros puede ser reclamado como de ambos). Observe que la mayor distancia que se puede alcanzar en el cuadrado original está dada por su diagonal, la cual mide $\sqrt{2}$ , luego en cada uno de los cuadrado pequeños la mayor distancia que se puede alcanzar es $\sqrt{2}$ /2, pero como los puntos P₁, P₂,..., P₅ están en el interior del cuadrado grande, la posibilidad de que uno de ellos sea un vértice no es posible, luego la distancia entre esos dos puntos es menor que $\sqrt{2}$ /2.

En el siguiente ejemplo, propuesto en la Olimpiada Mundial de 1972 (ver [2]), se muestra una simple extensión del principio de Dirichlet, la cual establece que ``si tenemos q^.n + 1 perlas y n cajas, entonces hay una caja que por lo menos tendrá más de q perlas".

Ejemplo 6. Dado cualquier conjunto de diez números naturales, donde cada uno de estos números está entre 1 y 99, inclusive. Demuestre que existen dos subconjuntos no vacíos del conjunto original, tal que la suma de sus elementos respectivos es igual.

Una vez elegido el conjunto de diez elementos es conocido que podemos formar la cantidad de 2¹⁰ - 1 = 1023 subconjuntos diferentes. Cada uno de estos subconjuntos tiene por suma de sus elementos a una cantidad menor que 1000, ya que lo peor que puede pasar es que escogiéramos al conjunto cuyos elementos son 90, 91,..., 99 y se tiene que

90 + 91 + ^... + 99 < 1000.

Por lo tanto, por el principio de Dirichlet (aquí las perlas son los 1023 subconjuntos y las cajas son los las cantidades que representan las sumas de estos subconjuntos, que son los números que van del 1 hasta antes del 1000) existen dos subconjuntos cuyas sumas de elementos son iguales, de hecho pueden haber muchos. Sin embargo, estos dos conjuntos podrían tener elementos comunes. Para conseguir que los conjuntos sean disjuntos lo que se hace es eliminar a los elementos comunes y considerar los nuevos conjuntos que no poseen esos elementos; además es obvio que si al inicio poseían igual suma de elementos, luego, al quitar los elementos comunes, siguen teneiendo la misma suma. Puede suceder que al eliminar los elementos comunes obtengamos conjuntos vacíos?

Los siguientes ejemplos son más difíciles que los anteriores, así que le pedimos al lector que los estudie y analice con sumo cuidado.

Ejemplo 7. En la sucesión 1, 1, 2, 3, 5, 8, 3, 1, 4,... cada término, empezando desde el tercero, es la suma de los dos términos anteriores, pero la adición se hace módulo 10. Pruebe que esta sucesión es periódica. Cuál es la máxima longitud posible del período?

Observemos que cualesquiera dos términos consecutivos de la sucesión determinan todos los términos siguientes y también todos los tréminos anteriores a ellos. Por lo tanto, la sucesión llegará a ser periódica si cualquier par (a, b) de términos sucesivos se repite, y el primer par que se repite deberá ser (1, 1).

Consideremos los 101 términos sucesivos de 1, 1, 2, 3, 5, 8, 3,.... Ellos forman 100 pares de números consecutivos, a saber, (1, 1),(1, 2),(2, 3),.... Como el par (0, 0) no puede ocurrir, tenemosque solamente 99 pares diferentes pueden existir, luego por el principio de Dirichlet dos de esos pares deberán repetirse y por lo tanto la sucesión será periódica. Además, el período de la sucesión es a sumo 99.

El siguiente ejemplo requiere un argumento más sofisticado.

Ejemplo 8. En una reunión hay seis personas. Muestre que necesariamente existen tres personas que se conocen mutuamente, o tres personas que no se conocen mutuamente (como en unejemplo anterior, admitimos que si a conoce a b, entonces b conoce a a).

Para resolver este problema nos valdremos del uso de la siguiente figura para ilustrar la situación.

Cada persona es representada por un vértice del hexágono. Cuando dos personas se conocen, ligamos los vértices con un segmento continuo; en caso contraio, usaremos un segmento discontinuo. Lo que debemos mostrar, usando esta figura, es que necesariamente existe un triángulo formado por líneas continuas o un triángulo formado por líneas discontinuas.

Consideremos los segmentos que inciden en un vértice llamado p₁. Como ellos son 5, entonces hay por lo menos tres que son continuos o por lo menos tres que son discontinuos. Admitamos que hay por lo menos tres continuos, de otra forma el argumento sería similar. Denotemso por p₂, p₃ y p₄ los vértices ligados con p₁ por medio de segmentos continuos (vea la siguiente figura). Si alguno de los segmentos p₂p₃, p₂p₄ 0 p₃p₄, es continuo entonces este segmento junto con los que ligan los extremos a p₁, forman un triángulo continuo. Por otra parte, si ninguno de ellos es continuo, entonces ellos forman un triángulo discontinuo. Lo cual completa la demostración.

Este ejemplo es un caso particular de un teorema más general, llamado el teorema de Ramsey. Dado cualquier entero k $\geq$ 3, existe un entero R(k) tal que en una reunión de R(k) personas, siempre existen k personas que se conocen mutuamente, o k que no se conocen mutuamente.

Ejemplo 9. Suponga que cada uno de los cuadrados de un tablero de dimensiones 4×7, como se muestra abajo, es coloreado ya sea de blanco o negro. Pruebe que no importa como se coloree, el tablero debe contener un rectángulo (formado por las líneas horizontales y verticales del tablero), tal como el que se muestra en la figura de abajo, cuyos cuadrados de las esquinas tienen todos el mismo color.

Tal rectánglo existe hasta sobre un tablero de dimensiones 3×7. Las configuraciones de colores de cada una de las columnas deben ser de uno de los tipos demostrados en la siguiente figura.

Suponga que una de las columnas es del tipo 1. El resultado estará probado si cualquiera de las seis columnas restantes es del tipo 1,2,3 ó 4. Supongamos que cada una de las otras columnas son del tipo 5,6,7 u 8. Entonces por el principio de Dirichlet, dos de las seis columnas deben tener el mismo tipo y el resultado está listo.

El mismo argumento aplica si una de las columnas es del tipo 8.

Ahora suponga que ninguna de las columnas son del tipo 1 u 8. Entonces, tenemos siete columnas del tipo 2,3,4,5,6 y 7, y por el principio de Dirichlet dos de las columnas deben ser del mismo tipo y el resultado está listo.

En el siguiente ejemplo se muestra una aplicación del principio de Dirichlet a una desigualdad. Este ejemplo apareció por primera vez en la final de la Olimpiada Canadiense de 1984.

Ejemplo 10. Dados siete números reales arbitrarios. Demuestre que existen dos de ellos, digamos x y y, tales que

La forma de la expresión anterior nos hace pensar en la función tangente. Es más, pensamos en la fórmula de la tangente de la suma de dos ángulos. Sean x₁,

x₂,..., x₇ los siete números elegidos al azar. Como la función f (x) = tanx es una biyección entre ] -/2,/2[ y IR, se sigue que para cada x_i existe un

tal que f ( ) =x_i, par i = 1, 2,...,7. Dividamos el intervalo ] -/2,/2[ en seis subintervalos de longitud /6. Por el principio de Dirichlet dos de los ,...,

pertenecen al mismo subintervalo. Sean estos dos números y , además supongamos, sin pérdida de generalidad, que $\leq$ , luego se sigue que

Recordando que tanx es creciente, se sigue que

y esta desigualdad es equivalente a

1 2 3 4 5 6

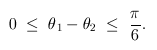
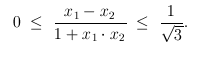
Revista digital Matemática, Educación e Internet.
Derechos Reservados