Principio de Dirichlet

| José Rosales O | Pedro Díaz N.  | Revista Digital Matemática, Educación e Internet |

 

1 2 3 4 5 6

Ejercicios

Esta sección está destinada a dar una cantidad importante de ejercicios, los cuales pondrán a prueba su habilidad para usar el Principio de Dirichlet. Como sugerencia se puede decir que absolutamente todos los ejercicios de esta sección pueden ser resueltos usando Dirichlet. Sin embargo, no dudamos de que hallan otras formas de resolverlos en donde no se use tal principio. Aún así, instamos al lector a que los resuelva exclusivamente usando el principio de Dirichlet.

1. Sea A cualquier conjunto de 20 enteros distintos, los cuales fueron elegidos de la progresión aritmética 1, 4, 7,..., 100. Pruebe que deben existir dos enteros distintos en A tal que su suma sea 104.

2. Considere nueve puntos de coordenadas enteras en IR³. Muestre que uno de los puntos medios, de los segmentos de recta definidos por los nueve puntos, también posee coordenadas enteras.

3. Sea x un número real arbitrario. Pruebe que entre los números
   x, 2x, 3x,...,(n - 1)x,
   existe uno, tal que su diferencia con un cierto entero es menor que 1/n.
4. Sean a₁, a₂,..., a_n enteros, no necesariamente distintos. Demuestre que siempre existe un subconjunto de estos números, cuya suma de elementos es divisible por n.

5. Si elegimos n + 1 números del conjunto {1, 2,..., 2n}, entonces hay dos que satisfacen que uno de ellos es divisible por el otro.

6. Sea n un entero positivo el cual no es divisible por 2 ni por 5. Pruebe que existe un múltiplo de n que consiste de puros unos.

7. Sean a, b, c, d enteros. Demuestre que el producto de las diferencias
   b - a, c - a, d - a, c - b, d - b, b - c,
   es divisible por 12.

8. Pruebe que, entre cualesquiera 13 números reales, existen dos, digamos x y y tales que
   

9. Considere un conjunto A con n elementos. Sea F una familia de subconjuntos de A tal que:
   • Cualesquiera dos elementos de F tienen intersección no vacía.
   • ningún otro subconjunto de A interseca todos los elementos de F.
   Se pide lo siguiente:
   1. Dé un ejemplo de una familia F que cumpla estas condiciones.
   2. Muestre que F posee 2^{n - 1} elementos.

10. Un disco cerrado de radio uno contiene siete puntos, cuyas distancias mutuas son 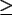$\geq$ 1. Pruebe que el centro del disco es uno de estos siete puntos.

1 2 3 4 5 6

Revista digital Matemática, Educación e Internet.
Derechos Reservados