Resumen
Se presenta una fórmula para el número de diagonales de un cubo, el cual es generado por vectores linealmente independientes, en n dimensiones y además se generaliza un teorema del álgebra lineal.
Introducción
El gran matemático Paul Erdös decía que un matemático
era aquel que estaba conjeturando y probando teoremas. En la tradición matemática
de nuestras universidades latinoamericanas, por cierto que muy poca, no se
acostumbra a inculcar este punto de vista. El presente artículo es producto
de este tipo de visión, la de Erdös. En la mayoría de cursos de álgebra
lineal que se imparten en nuestras universidades es común que se enuncie y
demuestre el siguiente teorema: "Dados dos vectores 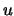 y
y 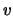 se cumple que:
se cumple que:
|
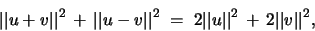
|
(1) |
La demostración de tal resultado es trivial, en efecto
El resultado anterior tine una interpretación geométrica
muy interesante. Recordemos que si los vectores 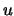 y
y 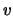 son linealmete independientes, entonces ellos generan un paralelogramo. Una de
las diagonales de dicho paralelogramo, la llamada principal, es dada por
son linealmete independientes, entonces ellos generan un paralelogramo. Una de
las diagonales de dicho paralelogramo, la llamada principal, es dada por 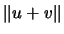 y la otra es dada por
y la otra es dada por 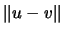 .
El teorema anterior establece que la suma de los cuadrados de las diagonales
de un paralelogramo es igual a dos veces la suma de los cuadrados de los lados
del paralelogramo. En este caso podemos concluir que en
.
El teorema anterior establece que la suma de los cuadrados de las diagonales
de un paralelogramo es igual a dos veces la suma de los cuadrados de los lados
del paralelogramo. En este caso podemos concluir que en 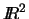 el 2-cubo, o paralelogramo, posee dos diagonales. La pregunta natural que
surge es: qué pasa en
el 2-cubo, o paralelogramo, posee dos diagonales. La pregunta natural que
surge es: qué pasa en 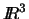 ?
La respuesta es interesante. Si tenemos tres vectores linealmente
independientes, digamos
?
La respuesta es interesante. Si tenemos tres vectores linealmente
independientes, digamos 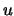 ,
,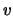 y
y 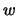 ,
podemos formar un cubo. En este caso el número de diagonales es cuatro. En
efecto, las diagonales son
,
podemos formar un cubo. En este caso el número de diagonales es cuatro. En
efecto, las diagonales son 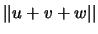 ,
,
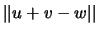 ,
,
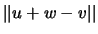 y
y 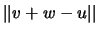 ,
no hay otras. Cuál es el análogo en
,
no hay otras. Cuál es el análogo en 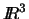 del teorema anterior? En
del teorema anterior? En 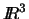 el teorema anterior diría que
el teorema anterior diría que
|
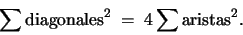
|
(2) |

