Con base en el teorema anterior podemos conjeturar el
siguiente teorema, el cual representa una extensión de la fórmula (1).
Teorema
Sea
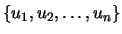 un conjunto de vectores linealmente independientes en
un conjunto de vectores linealmente independientes en 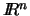 y sean
y sean
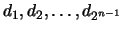 el número de diagonales del hiperparalelepípedo que es generado por los
el número de diagonales del hiperparalelepípedo que es generado por los 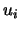 .
Entonces se cumple que
.
Entonces se cumple que
La demostración de este teorema procede en la siguiente forma. En primer
lugar, observemos que si desarrollamos el tÚrmino
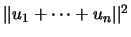 ,
obtenemos
,
obtenemos 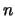 tÚrminos del tipo
tÚrminos del tipo 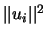 ,
donde
,
donde
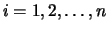 ,
y además
,
y además 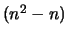 tÚrminos del tipo
tÚrminos del tipo 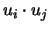 ,
para
,
para 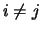 .
Esto se sigue del hecho, obvio por cierto, de que
.
Esto se sigue del hecho, obvio por cierto, de que
En segundo lugar, observemos que si desarrollamos un tÚrmino
del siguiente tipo
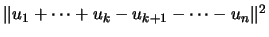 ,
obtenemos un total de
,
obtenemos un total de 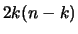 tÚrminos negativos de la forma
tÚrminos negativos de la forma 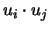 .
Observemos que el número de tÚrminos de la forma
.
Observemos que el número de tÚrminos de la forma 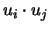 ,
donde
,
donde 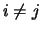 ,
al considerar la expresión
,
al considerar la expresión
es dado por
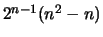 .
Esto se sigue de la primera observación, ya que por cada diagonal hay
.
Esto se sigue de la primera observación, ya que por cada diagonal hay 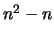 tÚrminos de la forma
tÚrminos de la forma 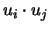 y en total hay
y en total hay 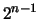 diagonales. Lo importante del artículo es demostrar que la mitad de estos tÚrminos
son negativos, es decir, los
diagonales. Lo importante del artículo es demostrar que la mitad de estos tÚrminos
son negativos, es decir, los 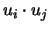 .
Para mostrar esto veamos que para
.
Para mostrar esto veamos que para 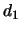 tenemos que
tenemos que
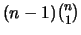 es la cantidad de tÚrminos negativos de la forma
es la cantidad de tÚrminos negativos de la forma 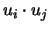 .
Para
.
Para 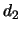 tenemos que la cantidad de tÚrminos negativos de la forma
tenemos que la cantidad de tÚrminos negativos de la forma 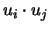 es dada por
es dada por
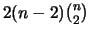 .
En general, el número de tÚrminos negativos de la forma
.
En general, el número de tÚrminos negativos de la forma 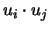 en
en 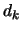 es dado por
es dado por
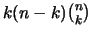 .
De lo anterior podemos concluir que el número de tÚrminos negativos de la
forma
.
De lo anterior podemos concluir que el número de tÚrminos negativos de la
forma 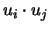 es dado por
es dado por
Del párrafo anterior se puede concluir la demostración de
nuestro teorema.

