Acerca de las diagonales del Hipercubo

| José Rosales O | Pedro Díaz N.  | Revista Digital Matemática, Educación e Internet |

 

 1 2 3 4

 

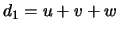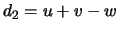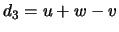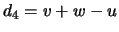La prueba de esto no es difícil, en efecto si denotamos $d_1= u+v+w $, $d_2=u+v-w$, $d_3=u+w-v$ y $d_4= v+w-u$, se sigue que

\begin{eqnarray*} \sum_{i=1}^4\vert\vert d_i\vert\vert^2 & = & d_1\cdot d_1 +... ... 4\vert\vert v\vert\vert^2 + 4 \vert\vert w\vert\vert^2. \end{eqnarray*}

De los dos casos anteriores podríamos conjeturar que el número de diagonales de un n-cubo o hipercubo, generado por 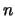$n$ vectores linealmente independientes, es 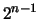$2^{n-1}$. Esto se establece en el siguiente teorema.

Teorema
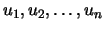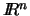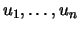Sean $u_1,u_2,\ldots,u_n$ vectores linealmente independientes en $I\!\!R^n$. Entonces el número de diagonales del cubo que generan los vectores $u_1,\ldots,u_n$ es dado por 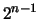$2^{n-1}$. La demostración de esto es elemental y usa combinatoria. Usaremos la siguiente notación. 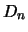$D_n$ denotará el número de diagonales que contienen un vector al que se le antepuso un signo menos. A partir de esto se tiene que

\begin{displaymath}D_0 \; = \; {n \choose 0},\;\; D_2 \;=\; {n \choose 1}, \; \ldots, D_n\; =\; {n \choose n}.\end{displaymath}

En resumen, el número total de diagonales(tómese en cuenta que se están contando dos veces cada una) en el hipercubo es:

\begin{eqnarray*} \mbox{N\'umero total de diagonales} & = & \frac{1}{2}\sum_{i=... ...}{2}(1 + 1)^n \\ & = & \frac{1}{2}2^n\\ & = & 2^{n-1}. \end{eqnarray*}