Regla y compás

| José Rosales O | Pedro Díaz N.  | Revista Digital Matemática, Educación e Internet |

1  2 3  4  5  6

La regla y el compás en la enseñanza

El programa oficial de secundaria contempla las siguientes construcciones básicas con regla y compás: la construcción de ángulos congruentes, construcción de la bisectriz de un ángulo, bisección de un segmento, mediatriz de un segmento, triángulo rectángulo, triángulo equilátero y las construcciones de las rectas notables y puntos de intersección de estas en un triángulo. En [3] y [4] podemos encontrar estas construcciones. Lloreth en [1] hace una recopilación más amplia de construcciones con regla y compás.

Se pueden utilizar estas construcciones básicas para realizar otras construcciones más complejas las cuales pueden ser asignadas a los estudiantes como trabajo extraclase. Algunas de las construcciones mencionadas en [8] algunas de estas son:

  1. Construir la recta tangente a un círculo desde un punto en una circunferencia.

    Esta construcción permite aplicar las construcciones de rectas perpendiculares a un segmento dado. Para su construcción sea K un círculo con centro O y sea P un punto de su circunferencia. Proceda a conectar los puntos O y P. Desde P, construya la recta perpendicular a OP (esta es una de las construcciones básicas ya apuntadas). Asi la recta obtenida es la recta buscada.

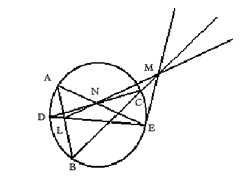
  2. Construir la recta tangentea un circulo desde un punto de su circunferencia,usando regla solamente

    Sea E un punto de la circunferencia dada. Escoja cuatro puntos diferentes A, B, C, D 2 de la circunferencia. Trace las rectas AB, BC, CD, DE, EA. Sea L la interseccion de AB con DE y sea N la intersección de CD con EA. Trace la recta LN y sea M su intersección con BC. La recta Buscada es la recta EM.

  3. Construir las dos rectas tangentes a un círculo dado desde un punto externo

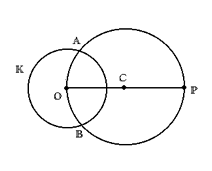
    Sea K un círculo con centro O( note que el centro del circulo se puede construir fácilmente), y sea P un punto externo a ello. Conecte OP y sea C el punto que biseca este segmento. Describa el círculo con centro C y radio CO. Sean A;B sus intersecciones con K. Las tangentes buscadas son las rectas PA y PB.

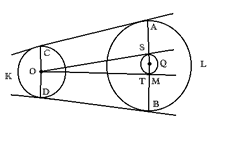
  4. Construir las tangentes comunes externas a dos círculos dados.

    Sean K y L dos círculos con respectivos centros O, Q y radios k y l. Supongamos, sin perdida de generalidad que k < l. Describa el círculo M de radio l - k y centro en Q. Construya las tangentes OS y OT desde O a M ( construcción anterior). Prolongue los radios QS y QT de M hasta cortar L en los puntos A y B respectivamente. Construya el radio OC de K paralelo a QA y al mismo lado de la recta OQ (construcción básica). Construya el radio OD de K paralelo a QB y al mismo lado de OQ. Conecte AC, BD. Estas últimas son las tangentes comunes a K y L.

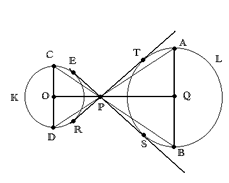
  5. Construir las tangentes comunes internas a dos círculos dados

    Sean k y L dos círculos con centros respectivos O, Q y radios k, l que no tienen intersección. Conecte OQ y construya los diámetros CD de K y AB de L perpendiculares a OQ tal que A y C queden del mismo lado de la recta OQ. Conewcte AD y BC. Sea P su punto de intersección. Construya las tangentes PE, PR a K y prolónguelas hasta tocar L en S y T. Las rectas ES y RT son las tangentes buscadas.

El lector puede observar que todas las construcciones hechas se basan en las construcciones básicas estudiadas en secundaria pero prenentan un nivel de dominio mayor. Estoe ejercicios sirven para repasar las construcciones vistas en clases pues durante su elaboración se deben de aplicar las construcciones vistas.

Otros ejercicios pueden ser consultados en [8]. Para construcciones usando solamente regla se puede consultar [7].

Revista digital Matemática, Educación e Internet.
Derechos Reservados