
|

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Visualizar una división de fracciones no es fácil. Lo que el programa Fracciones hace es tomar el denominador común, de modo que la división se expresa como
![]() . En esa notación es fácil ver que el resultado será
. En esa notación es fácil ver que el resultado será ![]() . El programa representará al divisor,
. El programa representará al divisor, ![]() , como el todo, y al dividendo,
, como el todo, y al dividendo, ![]() , como la parte. ¿Qué fracción es la parte del todo? La respuesta será el cociente,
, como la parte. ¿Qué fracción es la parte del todo? La respuesta será el cociente, ![]() .
.
Por ejemplo, para dividir
![]() se representan las dos fracciones con particiones verticales y se toma su denominador común:
se representan las dos fracciones con particiones verticales y se toma su denominador común:

Ya es fácil ver la respuesta: si la fracción derecha, ![]() , es el todo, y la izquierda,
, es el todo, y la izquierda, ![]() , es la parte, ¿qué fracción del todo es la parte? Pues tres (sextos) de cuatro (sextos):
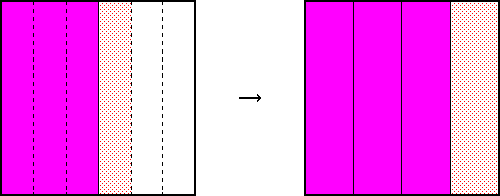
, es la parte, ¿qué fracción del todo es la parte? Pues tres (sextos) de cuatro (sextos): ![]() . El proceso de división se visualiza superponiendo las fracciones, observando la intersección, y extendiendo el divisor (el todo) para que llene el cuadrado unidad:
. El proceso de división se visualiza superponiendo las fracciones, observando la intersección, y extendiendo el divisor (el todo) para que llene el cuadrado unidad:
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Revista digital Matemática, Educación e Internet.
Derechos Reservados