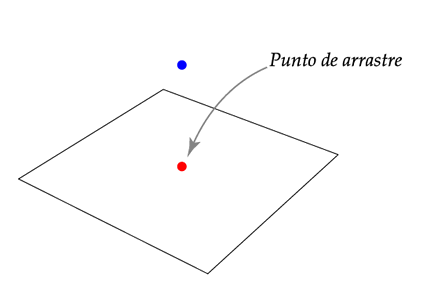
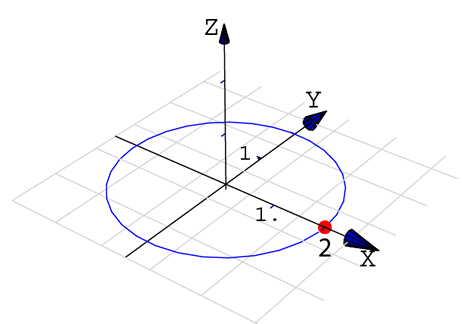
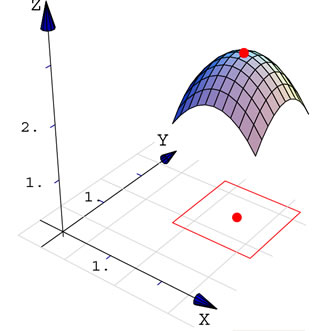
Variables independientes y variables dependientes
Un gráfico 'parametrizado' tiene objetos tales como puntos
Graphics3D[{ Point[{ x, y , x^2 + y^2 } ] }] }
con coordenadas 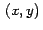
que pueden variar (con el arrastre del mouse)
Las coordenadas 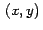 se deben inicializar para tener una imagen inicial.
Luego estas coordenadas se pueden "seleccionar con el mouse", a través de un punto,
de tal manera que al arrastrar el mouse, sus valores cambian. se deben inicializar para tener una imagen inicial.
Luego estas coordenadas se pueden "seleccionar con el mouse", a través de un punto,
de tal manera que al arrastrar el mouse, sus valores cambian.
Si una variable 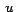 es variable independiente, su valor se puede modificar
seleccionando y arrastrando el mouse sobre un punto que tiene al menos una vez la coordenada es variable independiente, su valor se puede modificar
seleccionando y arrastrando el mouse sobre un punto que tiene al menos una vez la coordenada 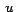 (limpia). (limpia).
Las variables independientes se declaran con una lista de reglas que inicializan las variables
independentVariables = {x -> 2, y -> 2}
En este caso, el punto Point[{x,y,0}] se puede seleccionar y "arrastrar"
.
El punto Point[{1.*x,1.*y, 2}] no se puede seleccionar ni arrastrar pues las variables independientes no aparecen
"limpias". Sin embargo al arrastrar Point[{x,y,2}], el punto Point[{1.*x,1.*y, 2}]
se mueve en función del primer punto. En realidad, las expresiones '1.*x' , '1.*y' son variables dependientes.
Las variables dependientes son variables que cambian en función de los valores de
las variables independientes o son constantes.
Las variables dependientes se declaran con una lista de reglas. Por
ejemplo las variables dependientes xi
y yi se pueden
declarar en función de las variables independientes
x y
y.
dependentVariables = {xi -> x/2, yi -> Sqrt[y]}
También una variable dependiente puede
depender de otra variable dependiente anterior, en la lista de reglas de las variables dependientes
También se usan reglas para definir el comportamiento de las variables
independientes pero en la lista de reglas de las variables dependientes.
Estas reglas usan expresiones (de Mathematica) simples.
Por ejemplo, si queremos que la variable 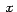 solo se desplace entre 0 y 1, lo que hacemos es
asignarle valor cero si estamos en un valor negativo y asignarle el valor 1 si estamos en un valor mayor que uno y
en otro caso, el valor actual: solo se desplace entre 0 y 1, lo que hacemos es
asignarle valor cero si estamos en un valor negativo y asignarle el valor 1 si estamos en un valor mayor que uno y
en otro caso, el valor actual:
dependentVariables = {x -> If[ x < 0 , 0, If[ x > 1, 1, x] ]}
Este conjunto de reglas se pueden usar para implementar el gráfico en Mathematica
pero se deben indicar y se pueden variar en los parámetros del applet que levanta el gráfico
Por ejemplo, si queremos que un punto 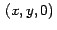 se mueva sobre un rectángulo se mueva sobre un rectángulo
![$\,[0,4] \times [0,4]\,$](img5.gif) ,
declaramos las variables independientes ,
declaramos las variables independientes 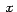 e e 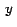 , luego las inicializamos y después definimos
su comportamiento con reglas , luego las inicializamos y después definimos
su comportamiento con reglas
independentVariables = {x -> 2, y -> 2};
dependentVariables = {x -> If[x < 0, 0, If[x > 4, 4, x]],
y -> If[y < 0, 0, If[y > 4, 4, y]]};
punto = { AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{x, y, 0}], (*---> punto de arrastre, se puede seleccionar*)
Point[{1.*x, 1.*y, 1}],(*---> punto dependiente,No seleccionable*)
};
g = Graphics3D[{punto}];
Show[N[g] //. Join[independentVariables, dependentVariables]]; |
|
Esto debe quedar plasmado en los parámetros del applet
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x->2,y->2}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{x->If[x<0,0,If[x>4,4,x]],y->If[y<0,0,If[y>4,4,y]]}'>
Veamos el ejemplo completo
Ejemplo 1
Arrastrar un punto 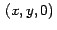 , inicializado con , inicializado con
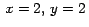 , sobre el rectángulo , sobre el rectángulo
![$\,[0,4] \times [0,4]\,$](img5.gif)
El código completo incluye la implementación del gráfico y generar la página Web.
Vamos a suponer que el archivo live.jar está en la carpeta
C:\MisLG3D y
que ahí quedará también la página Web
(*----------------------------- Gráfico -----------------------------*)
independentVariables = {x -> 2, y -> 2};
dependentVariables = {x -> If[x < 0, 0, If[x > 4, 4, x]],
y -> If[y < 0, 0, If[y > 4, 4, y]]};
puntos = {AbsolutePointSize[6],
RGBColor[1, 0, 0], Point[{x, y, 0}],
RGBColor[0, 0, 1], Point[{1.*x, 1.*y, 2}]};
rectangulo = {Line[{{0, 0, 0}, {4, 0, 0}, {4, 4, 0}, {0, 4, 0}, {0, 0,0}}]};
g = Graphics3D[{rectangulo, puntos},
Boxed -> False,
ViewPoint -> {1.761, -2.313, 1.732}
];
(*ver el gráfico en Mathematica*)
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*----------------------------- página Web -----------------------------*)
(* Generar la página Web 'ejemplo1.html'. *)
(* El archivo ejemplo1.m es el archivo de coordenadas *)
WriteLiveForm["ejemplo1.m", g, Dir -> "C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo1.html"];
(* código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=150 width=200 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo1.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x->2,y->2}'>
<PARAM NAME=DEPENDENT_VARIABLES \
VALUE='{x->If[x<0,0,If[x>4,4,x]],y->If[y<0,0,If[y>4,4,y]]}'>
</APPLET>
</BODY></HTML>";
(* escribir en el archivo*)
WriteString[strm, pagina];
Close[strm];
|
|
Restringiendo el arrastre sobre una curva o sobre una superficie
Podemos usar la lista de reglas de las variables dependientes para
restringir el recorrido de un punto. Lo que hacemos es redefinir
las variables independientes de tal manera que cumplan las
ecuaciones de la curva o la superficie.
Cuando seleccionamos un
punto con variables independientes 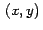 y arrastramos el
mouse, sobre cualquier sector de la pantalla, el punto de pantalla
es proyectado sobre el plano XY (o un plano paralelo al plano XY).
Así, si rotamos el gráfico y ponemos el plano XY de frente,
entonces el punto y arrastramos el
mouse, sobre cualquier sector de la pantalla, el punto de pantalla
es proyectado sobre el plano XY (o un plano paralelo al plano XY).
Así, si rotamos el gráfico y ponemos el plano XY de frente,
entonces el punto 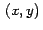 puede ser aproximadamente igual al
punto de proyección puede ser aproximadamente igual al
punto de proyección 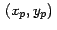 . En todo caso, la idea es usar
reglas para usar el punto . En todo caso, la idea es usar
reglas para usar el punto 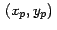 para redefinir el punto para redefinir el punto
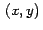 de tal manera que esté en la curva o en la superficie
que deseamos. de tal manera que esté en la curva o en la superficie
que deseamos.
En el primer ejemplo vamos a usar coordenadas polares para
restringir el recorrido de un punto a una circunferencia. El el
segundo ejemplo vamos a usar directamente la ecuación de la
superficie, en coordenadas rectangulares, para lograr que un punto
recorra una superficie.
Ejemplo 2
Arrastrar un punto sobre la circunferencia
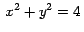 . .
Si 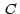 es la circunferencia en es la circunferencia en
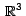 , en Mathematica , en Mathematica 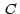 se parametriza así se parametriza así
es decir,
![$\,x = 2*\mbox{Cos}[t], \, y=2*\mbox{Sin}[t]\,$](img13.gif) y y
![$\,t = \mbox{ArcTan}[x,y].\,$](img14.gif)
Dichosamente ArcTan devuelve el ángulo de acuerdo al cuadrante en el que se encuentra el punto 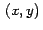 . .
Estas ecuaciones las usaremos para restringir el recorrido del
punto 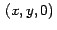 de la siguiente manera: cuando el mouse
selecciona el punto de la siguiente manera: cuando el mouse
selecciona el punto 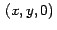 en la pantalla y se produce el
arrastre, el punto actual en pantalla es proyectado, sobre
el plano XY, digamos en el punto en la pantalla y se produce el
arrastre, el punto actual en pantalla es proyectado, sobre
el plano XY, digamos en el punto 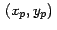 . Calculamos el
ángulo . Calculamos el
ángulo
![$\,t = \mbox{ArcTan}[x_p,y_p]\,$](img15.gif) y redefinimos y redefinimos 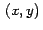 usando las ecuaciones
usando las ecuaciones
![$\,x = 2*\mbox{Cos}[t], \, y=2*\mbox{Sin}[t]\,$](img13.gif) y y
![$\,t = \mbox{ArcTan}[x,y].\,$](img14.gif) Es claro que el punto Es claro que el punto 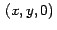 estará en la circunferencia.
estará en la circunferencia.
En código, esto se vería así
independentVariables = {x
-> 2, y -> 0};
dependentVariables = {theta -> ArcTan[x, y],
x -> 2*Cos[theta],
y -> 2*Sin[theta]
}; |
|
Observe que si ponemos la circunferencia de frente, el arrastre del punto con el mouse parecerá muy natural
pues la proyección del punto de pantalla sobre el plano XY puede coincidir con el punto, es decir
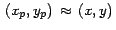 . .
Si rotamos la figura, el arrastre del
punto puede presentar alguna dificultad debido a las restricciones a las que se ve sometida la proyección
sobre el plano XY.
El código completo es el siguiente
independentVariables = {x
-> 2, y -> 0};
dependentVariables = {
theta -> ArcTan[x, y],
x -> 2*Cos[theta],
y -> 2*Sin[theta]
};
circulo = Line[Table[{0 + 2*Cos[t], 0 + 2*Sin[t], 0} , {t, 0, 2Pi, 0.2}]];
punto = {
AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[{x, y, 0}]
};
g = Graphics3D[{Ejes[-02.5, 3, -2.5, 3, -0.1, 3], punto,
RGBColor[0, 0, 1], circulo},
Boxed -> False, ViewPoint -> {1.761, -2.313, 1.732}];
Show[N[g] //. Join[independentVariables,dependentVariables]];
(*página Web*)
WriteLiveForm["ejemplo3.m", g, Dir ->
"C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo3.html"];
(*código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=400 width=400 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo3.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x->2,y->0}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{
theta ->ArcTan[x,y],
x-> 2*Cos[theta],
y->2*Sin[theta]
}'>
</APPLET>
</BODY></HTML>";
WriteString[strm, pagina];
Close[strm]; |
|
Ejemplo 3
Arrastrar un punto sobre el trozo de superficie
![$\,S: \; \; \;
(x-2)^2 + (y - 2)^2+\,z \,-3 = \,0, \; \; \;
(x,y) \, \in \, [1.25, \, 2.75] \times [1.25, \, 2.75].\,$](img17.gif)
El intervalo escogido es solo para ver mejor la superficie.
En este ejemplo hay dos elementos:
- tomar un punto de la superficie
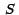 y 'pasearlo' por la superficie y 'pasearlo' por la superficie
- definir un dominio de acción: solo se consideran puntos
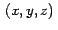 de la superficie
de la superficie 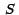 con pre-imagen con pre-imagen 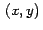 en el cuadrado en el cuadrado
![$\,[1.25, \, 2.75] \times [1.25, \, 2.75]\,$](img20.gif)
Debemos hacer lo siguiente:
- definir las variables independientes: inicializarlas de tal manera que coorespondan a punto sobre
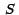
- definir su comportamiento para que, al arrastrar el punto, no nos salgamos de la superficie
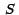
- definir su comportamiento para que las pre-imagen
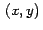 no se salga del dominio no se salga del dominio
![$\,[1.25, \, 2.75] \times [1.25, \, 2.75]\,$](img20.gif)
- Implementar un sistema de ejes 3D
- implementar la superficie
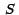
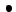 - Observemos que
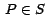 si si
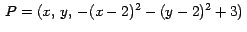 , así que para
restringir el punto al rectángulo y a la superficie se usarán las reglas , así que para
restringir el punto al rectángulo y a la superficie se usarán las reglas
independentVariables = {x -> 2, y -> 2};
dependentVariables = {
x -> If[x < 1.25, 1.25, If[x > 2.75, 2.75, x]],
y -> If[y < 1.25, 1.25, If[y > 2.75, 2.75, y]],
z -> -(x - 2)^2 - (y - 2)^2 + 3
}; |
|
 - En el código que sigue aparece el siguiente código
puntos =
{AbsolutePointSize[6], RGBColor[1, 0, 0],
Point[{x, y, z}], (*----> punto de arrastre sobre S*)
Point[{1.*x, 1.*y, z + 0.01}], Point[{1.*x, 1.*y, z - 0.01}],
Point[{x, y, 0}] (*----> pre-imagen es también punto de arrastre*)
}; |
|
Los puntos Point[{1.*x, 1.*y, z + 0.01}] y Point[{1.*x, 1.*y, z - 0.01}],
son dos puntos que se usan
previendo el ocultamiento del punto Point[{x, y, z}] por
los polígonos
de la superficie.
 - El ejemplo usa la biblioteca 'DrawGraphics' para los ejes 3D. Puede consultar el
número
anterior de la revista para ver su uso.
El código completo es el siguiente
|
(*------------------------------- ejes 3D ------------------------------*)
Needs["DrawGraphics`DrawingMaster`"];
(* Ejes 3D *)
Ejes[xmin_, xmax_, ymin_, ymax_, zmin_, zmax_] := {
(*Flechas*)
SurfaceColor[RGBColor[0, 0, 1]],
ArrowLine3D[{{xmin, 0, 0}, {0, 0, 0}, {xmax, 0, 0}}],
ArrowLine3D[{{0, ymin, 0}, {0, 0, 0}, {0, ymax, 0}}],
ArrowLine3D[{{0, 0, zmin}, {0, 0, 0}, {0, 0, zmax}}],
Text[
StyleForm["X", FontSize -> 12, FontWeight -> "Bold"], {xmax, -0.3,
0}],
Text[
StyleForm["Y", FontSize -> 12, FontWeight -> "Bold"], {-0.3, ymax,
0.1}],
Text[
StyleForm["Z", FontSize -> 12, FontWeight -> "Bold"], {0, -0.2,
zmax}],
(* numeros *)
Table[Text[i, {i, -0.3, 0}], {i, 1, xmax - 2, 1}],
Table[Text[i, {-0.3, i, 0}], {i, 1, ymax - 2, 1}],
Table[Text[i, {-0.3, -0.3, i}], {i, 1, zmax - 2, 1}],
RGBColor[0, 0, 0.627451],
(* rayitas *)
Table[Line[{{-0.1, i, 0}, {0, i, 0}}], {i, 1, ymax - 1, 1}],
Table[Line[{{i, -0.1, 0}, {i, 0, 0}}], {i, 1, xmax - 1, 1}],
Table[Line[{{0, -0.1, i}, {0, 0, i}}], {i, 1, zmax - 1, 1}],
(*grid*)
GrayLevel[0.843137],
Table[Line[{{xmin, i, 0}, {xmax, i, 0}}], {i, ymin, ymax, 1}],
Table[Line[{{i, ymin, 0}, {i, ymax, 0}}], {i, xmin, xmax, 1}]
};
(*------------------------------- Gráfico ------------------------------*)
independentVariables = {x -> 2, y -> 2};
dependentVariables = { x -> If[x < 1.25, 1.25, If[x > 2.75, 2.75, x]],
y -> If[y < 1.25, 1.25, If[y > 2.75, 2.75, y]],
z -> -(x - 2)^2 - (y - 2)^2 + 3
};
(*Parabolide*)
minx = 1.25; miny = 1.25; maxx = 2.75; maxy = 2.75;
n = 10;
dx = (maxx - minx)/n;
dy = (maxy - miny)/n;
f[vx_, vy_] = -(vx - 2)^2 - (vy - 2)^2 + 3;
paraboloid = Table[Polygon[{{i , j , f[i, j]},
{i + dx , j , f[(i + dx), j]},
{i + dx , j + dy ,f[(i + dx), (j + dy)]},
{i ,j + dy ,f[i, (j + dy)]}}],
{i, minx, maxx - dx/2, dx},
{j, miny, maxy - dy/2, dy}];
(*Punto(s) *)
puntos = {AbsolutePointSize[6], RGBColor[1, 0, 0],
Point[{x, y, z}], (*----> punto de arrastre *)
Point[{1.*x, 1.*y, z + 0.01}], Point[{1.*x, 1.*y, z - 0.01}],
Point[{x, y, 0}] (*----> pre-imagen*)
};
rectangulo = {Line[{{1.25, 1.25, 0}, {2.75, 1.25, 0}, {2.75, 2.75, 0},
{1.25,2.75, 0}, {1.25, 1.25, 0}}]
};
g = Graphics3D[{Ejes[-0.5, 3, -0.5, 3, -0.1, 4], paraboloid, puntos,
RGBColor[1, 0, 0], rectangulo},
Boxed -> False,
ViewPoint -> {1.761, -2.313, 1.732},
PlotRange -> All,
AspectRatio -> Automatic];
(*ver el gráfico*)
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*----------------------------- página Web -----------------------------*)
WriteLiveForm["ejemplo2.m", g, Dir -> "C:\\MisLG3D\\"];
(* Crea la página Web *)
SetDirectory["C:\\MisLG3D\\"];
strm = OpenWrite["ejemplo2.html"];
(*código de la página Web*)
pagina = "<HTML><HEAD></HEAD> <BODY>
<APPLET height=400 width=400 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo2.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x->2,y->2}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{
x->If[x<1.25,1.25,If[x>2.75,2.75,x]],
y->If[y<1.25,1.25,If[y>2.75,2.75,y]],
z->-(x-2)^2 -(y-2)^2+3}'>
</APPLET>
</BODY></HTML>";
WriteString[strm, pagina];
Close[strm];
|
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|