|
Interpretación geométrica de algunos conceptos del cálculo en varias variables
Vector tangente
En esta sección vamos a implementar el vector tangente a una
curva. De aquí se puede saltar de manera sencilla a otros
conceptos como derivada direccional y plano tangente.
Recordemos que si un curva suave 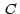 está parametrizada
por está parametrizada
por
![$\,r(t)=(\,x(t),\,y(t),\,z(t)\,)\; \; \mbox{con}\; \; t \in
[a,b],\,$](img40.gif) el vector tangente en el vector tangente en 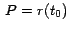 es es
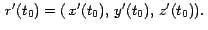
La implementación de la curva 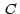 podría ser podría ser
curvaC = Line[Table[{x(t),y(t),z(t)}, {t, a, b, 0.1}]];
mientras que el vector tangente lo podemos implementar usando
Arrow3D[] de la biblioteca DrawGraphics
independentVariables = {t -> t0};
P = {x(t) , y(t) , z(t) };
vT = {x'(t), y'(t) , z'(t)};
vTT=Arrow3D[P,P + vT];
g=Graphics3D[{Point[P], curvaC, vvT}]; |
|
Ejemplo 9
Graficar la curva
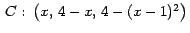 con con
![$\,x \in [0,3]\,$](img44.gif) y el vector tangente a y el vector tangente a 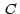 en un punto de
arrastre en un punto de
arrastre 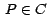
(*------------------------------- Gráfico ------------------------------*)
SetOptions[Arrow3D, HeadScaling3D-> 1, HeadLength3D -> 0.3];
independentVariables = {x -> 1, y ->1};
dependentVariables = {};
P = {x, 4 - x, 4 - (x - 1)^2}; (*puntos de la curva*)
vT = {1,-1, -2(x - 1)}; (*vector tangente *)
curva =Line[Table[{t, 4 - t, 4 - (t - 1)^2}, {t, 0, 3, 0.2}]];
vTT = Arrow3D[P, P + vT];
punto = { AbsolutePointSize[6],
RGBColor[1, 0, 0],
Point[P]
};
g = Graphics3D[{
Ejes[-0.5, 5, -0.5, 5, -0.1, 5],
punto, RGBColor[0, 0, 1],
AbsoluteThickness[2],
RGBColor[0.0588235, 0.52549, 0.0705882],
vTT,
RGBColor[0, 0, 1],
curva},
Boxed -> False,
ViewPoint -> {3.096, 0.100, 1.095},
PlotRange -> All
];
Show[N[g] //. Join[independentVariables, dependentVariables]];
(*----------------------------- página Web -----------------------------*)
(* Generar la página Web 'ejemplo7.html'. *)
(* El archivo ejemplo7.m es el archivo de coordenadas *)
WriteLiveForm["ejemplo7.m",g,Dir\[Rule]"C:\\MisLG3D\\"];
SetDirectory["C:\\MisLG3D\\"];
strm=OpenWrite["ejemplo7.html"];
(*código de la página Web*) pagina="<HTML><HEAD></HEAD> <BODY>
<APPLET height=400 width=400 archive=live.jar code=Live.class >
<PARAM NAME=INPUT_FILE VALUE = ejemplo7.m >
<PARAM NAME=INDEPENDENT_VARIABLES VALUE='{x->1}'>
<PARAM NAME=DEPENDENT_VARIABLES VALUE='{x->If[x<0,0,If[x>3,3,x]]}'>
</APPLET>
</BODY></HTML>";
WriteString[strm,pagina];
Close[strm];
|
|
Derivada direccional y plano tangente
Para la implementación de la interpretación geométrica de la
derivada direccional, necesitamos una superficie suave 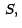 un punto un punto 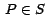 y un vector y un vector
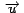 . Usamos el
hecho (geométrico) de que la recta tengente a . Usamos el
hecho (geométrico) de que la recta tengente a 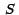 en en 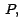 en la dirección de en la dirección de
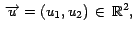 es la recta tangente en
es la recta tangente en 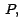 a la curva a la curva 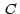 de intersección entre el plano generado por la recta de intersección entre el plano generado por la recta
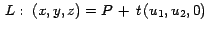 y la superficie y la superficie 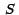 . Por tanto podemos usar el código
del ejemplo anterior. . Por tanto podemos usar el código
del ejemplo anterior.
Para el caso del plano tangente a 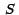 en en 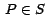 , observamos que este plano , observamos que este plano 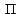 tiene ecuación vectorial tiene ecuación vectorial
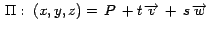 .
Podemos escoger .
Podemos escoger
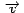 como el vector tangente a como el vector tangente a 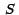 en en 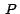 ,
en la dirección del eje X, o sea en la dirección de ,
en la dirección del eje X, o sea en la dirección de
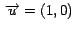 y y
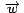 como el vector tangente a como el vector tangente a 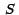 en en 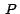 ,
en la dirección del eje Y, o sea en la dirección de ,
en la dirección del eje Y, o sea en la dirección de
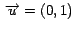
Conclusión
A través de los ejemplos se han presentado las ideas básicas de cómo usar LiveGraphics3D
para generar gráficos parametrizados. Los parámetros se declaran como variables independientes
y su valor cambia arrastrando puntos que los contienen en sus coordenadas (de manera limpia). Las posibilidades
de programación están limitadas por las expresiones que reconoce LG3D que, en particular, no admite
constructores de listas ni control de flujos. Aún así se pueden crear gráficos
parametrizados de gran complejidad.
Bibliografía
| 1 |
Martin, Kraus. LiveGraphics3D. Consultada 24 mar. 2005. Disponible en
http://wwwvis.informatik.uni-stuttgart.de/~kraus/LiveGraphics3D/index.html |
| 2 |
Pita R. C. 1995. Cálculo Vectorial. Prentice-Hall. México, MX, 1078 p.
|
| 3 |
Davis, B.1994. Calculus and Mathematica. Addison-Wesley. New York, US, 330p. |
| 4 |
Schneider, Ph. Eberly, D. 2003. Geometric Tools for Computers Graphics. Ed. Morgan Kaufmann.
San Francisco California. 1007 |
| 5 |
Wolfram Research. Consultado 20 de mayo 2005. Disponible en http://www.wolfram.com
|
| 6 |
LiveGraphics3d Home. Consultado 20 de mayo de 2005. Disponible en
http://www.vis.informatik.uni-stuttgart.de/ kraus/LiveGraphics3D/
|
| 7 |
Arrow3D. Consultado 20 de mayo 2005. Disponible en http://library.wolfram.com/infocenter/TechNotes/4117/ |
| 8 |
DrawGraphics. Consultado 20 de mayo 2005. Disponible en http://home.earthlink.net/ djmp/Mathematica.html |
Este documento
fue generado usando
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|
|